College Algebra (Italiano)
Risultati dellapprendimento
- Identifica il vertice, lasse di simmetria, lintercetta y e il valore minimo o massimo di una parabola da è un grafico.
- Identifica una funzione quadratica scritta in forma generale e vertice.
- Data una funzione quadratica in forma generale, trova il vertice.
- Definisci il dominio e lintervallo di una funzione quadratica identificando il vertice come massimo o minimo.
Il grafico di una funzione quadratica è una curva a forma di U chiamata parabola. Una caratteristica importante del grafico è che ha un punto estremo, chiamato vertice. Se la parabola si apre, il vertice rappresenta il punto più basso del grafico, o il valore minimo della funzione quadratica. Se la parabola si apre verso il basso, il vertice rappresenta il punto più alto del grafico o il valore massimo. In entrambi i casi, il vertice è un punto di svolta nel grafico. Il grafico è anche simmetrico con una linea verticale tracciata attraverso il vertice, chiamata asse di simmetria.
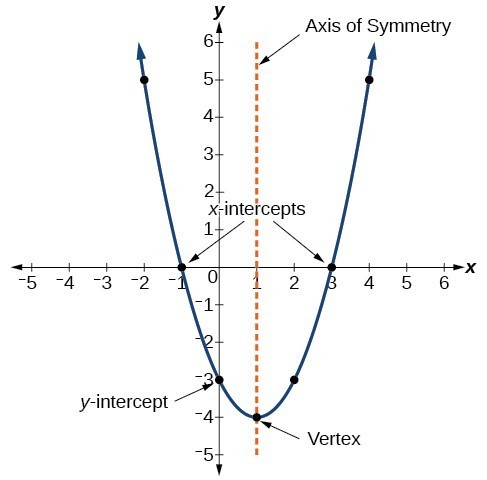
Equazioni di funzioni quadratiche
La forma generale di una funzione quadratica presenta la funzione nella forma
f \ left (x \ right) = a {x} ^ {2} + bx + c
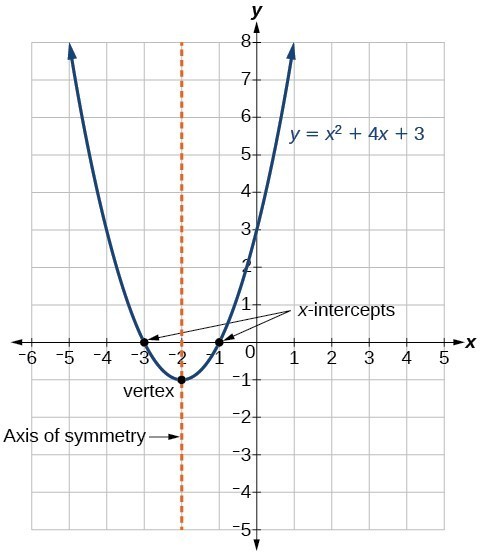
La forma standard di una funzione quadratica presenta la funzione nella forma
f \ left (x \ right) = a {\ left (xh \ right)} ^ {2} + k
Data una funzione quadratica in generale form, trova il vertice della parabola.
Una ragione per cui potremmo voler identificare il vertice della parabola è che questo punto ci informerà dove si verifica il valore massimo o minimo delloutput, k, e dove si verifica, h. Se ci viene data la forma generale di una funzione quadratica:
f (x) = ax ^ 2 + bx + c
Possiamo definire il vertice, (h, k), effettuando le seguenti operazioni:
Trovare il dominio e lintervallo di una funzione quadratica
Qualsiasi numero può essere il valore di input di una funzione quadratica. Quindi il dominio di qualsiasi funzione quadratica è tutti i numeri reali. Poiché le parabole hanno un massimo o un minimo al vertice, lintervallo è limitato. Poiché il vertice di una parabola sarà un massimo o un minimo, lintervallo sarà composto da tutti i valori y maggiori o uguali alla coordinata y del vertice o minori o uguali alla coordinata y al punto di svolta , a seconda che la parabola si apra o si apra.
Contribuisci!
Migliora questa paginaUlteriori informazioni