College Algebra (Italiano)
Guardando il grafico di una funzione razionale, possiamo investigare il suo comportamento locale e vedere facilmente se ci sono asintoti. Potremmo persino essere in grado di approssimare la loro posizione. Anche senza il grafico, tuttavia, possiamo ancora determinare se una data funzione razionale ha degli asintoti e calcolare la loro posizione.
Asintoti verticali
Gli asintoti verticali di una funzione razionale possono essere trovato esaminando i fattori del denominatore che non sono comuni ai fattori del numeratore. Gli asintoti verticali si verificano agli zeri di tali fattori.
Procedura: data una funzione razionale, identificare eventuali asintoti verticali del suo grafico.
- Fattorizzare il numeratore e denominatore.
- Notare eventuali restrizioni nel dominio della funzione.
- Ridurre lespressione annullando i fattori comuni nel numeratore e nel denominatore.
- Annotare eventuali valori che fanno sì che il denominatore sia zero in questa versione semplificata. Questi sono i punti in cui si verificano gli asintoti verticali.
- Notare qualsiasi restrizione nel dominio in cui non si verificano gli asintoti. Queste sono discontinuità rimovibili.
Discontinuità rimovibili
Occasionalmente, un grafico conterrà un buco: un singolo punto in cui il grafico non è definito, indicato da un cerchio aperto. Chiamiamo tale buco una discontinuità rimovibile.
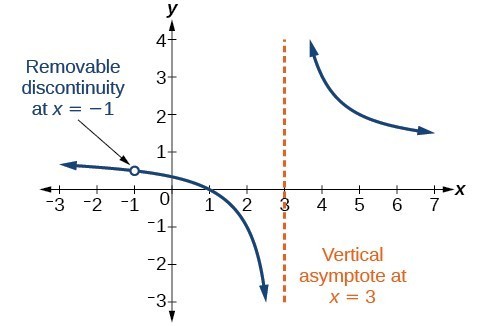
Figura 10
Una nota generale: discontinuità rimovibili di funzioni razionali
Una discontinuità rimovibile si verifica nel grafico di una funzione razionale in x = a se a è zero per un fattore al denominatore comune a un fattore al numeratore. Fattorizziamo numeratore e denominatore e controlliamo i fattori comuni. Se ne troviamo uno, poniamo il fattore comune uguale a 0 e risolviamo. Questa è la posizione della discontinuità rimovibile. Ciò è vero se la molteplicità di questo fattore è maggiore o uguale a quella al denominatore. Se la molteplicità di questo fattore è maggiore nel denominatore, allora cè ancora un asintoto a quel valore.
Asintoti orizzontali
Mentre gli asintoti verticali descrivono il comportamento di un grafico quando loutput diventa molto grande o molto piccolo, gli asintoti orizzontali aiutano a descrivere il comportamento di un grafico quando linput diventa molto grande o molto piccolo. Ricorda che il comportamento finale di un polinomio rispecchierà quello del termine principale. Allo stesso modo, il comportamento finale di una funzione razionale rispecchierà quello del rapporto tra i termini iniziali delle funzioni numeratore e denominatore.
Ci sono tre risultati distinti quando si controllano gli asintoti orizzontali:
Caso 1: se il grado del denominatore > grado del numeratore, è presente un asintoto orizzontale in y = 0.

Caso 2: se il grado del denominatore < grado del numeratore per uno, otteniamo un asintoto inclinato.

Si noti che, mentre il grafico di una funzione razionale non attraverserà mai un asintoto verticale, il grafico può o non può attraversare un orizzontale o asintoto inclinato. Inoltre, sebbene il grafico di una funzione razionale possa avere molti asintoti verticali, il grafico avrà al massimo un asintoto orizzontale (o inclinato).
Va notato che, se il grado del numeratore è maggiore rispetto al grado del denominatore di più di uno, il comportamento finale del grafico imiterà il comportamento della frazione di comportamento finale ridotta. Ad esempio, se avessimo la funzione
con comportamento finale
il comportamento finale del grafico sarebbe simile a quello di un polinomio pari con un coefficiente iniziale positivo.
Nota generale: asintoti orizzontali di Funzioni razionali
Lasintoto orizzontale di una funzione razionale può essere determinato osservando i gradi del numeratore e del denominatore.
- Il grado del numeratore è inferiore al grado del denominatore: asintoto orizzontale in y = 0.
- Il grado del numeratore è maggiore del grado del denominatore di uno: nessun asintoto orizzontale; asintoto obliquo.
- Il grado del numeratore è uguale al grado del denominatore: asintoto orizzontale al rapporto dei coefficienti principali.
Una nota generale: intercettazioni di funzioni razionali
Una funzione razionale avrà unintercetta y quando linput è zero, se il la funzione è definita a zero. Una funzione razionale non avrà unintercetta y se la funzione non è definita a zero.
Allo stesso modo, una funzione razionale avrà intercette x agli input che fanno sì che loutput sia zero. Poiché una frazione è uguale a zero solo quando il numeratore è zero, le intercettazioni x possono verificarsi solo quando il numeratore della funzione razionale è uguale a zero.
Prova 7
Data la funzione reciproca al quadrato che è spostata a destra di 3 unità e in basso di 4 unità, scrivila come una funzione razionale. Quindi, trova le intercette x e y e gli asintoti orizzontali e verticali.
Soluzione