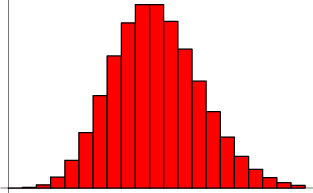
Poisson-folyamat alapján annak valószínűségét, hogy pontosan sikereket érj el a próbákban, a binomiális eloszlás határa adja meg

(1)

Az eloszlás megtekintése a várható sikerek számának függvényében

(2)

a minta mérete helyett a fix esetén a (2) egyenlet ekkor

(3)

Ha a minta mérete nagy lesz, akkor az eloszlás megközelíti

			(4)
			(5)
			(6)
			(7)
			(8)

amely Poisson-eloszlás néven ismert (Papoulis 1984, 101. és 554. o .; Pfeiffer és Schum 1973, p. 200). Vegye figyelembe, hogy a (z) minta mérete teljesen kiesett a valószínűségi függvényből, amelynek ugyanaz a funkcionális formája van a összes értékénél. / p>

A Poisson-eloszlást a WolframLanguage PoissonDistribution-ként valósítja meg.

A várakozásoknak megfelelően a Poisson-eloszlást normalizáljuk úgy, hogy a valószínűségek összege 1 legyen, mivel

(9 )

A valószínűségek arányát a következő adja:

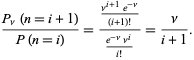(10)

A Poisson-eloszlás akkor éri el a maximumot, amikor

(11)

ahol az Euler-Mascheroni konstans, a egy harmonikus szám, amely a transzcendentális egyenlethez vezet

(12)

amelyet nem lehet pontosan megoldani a esetén.

APoisson-eloszlás pillanatgeneráló függvényét a

			(13)
			(14)
			(15)
			(16)
			(17)
			(18)

tehát

			(19)
			(20)

(Papoulis 1984, p. 554).

A nyers pillanatokat közvetlenül is összegezhetjük összegzéssel, ami váratlan kapcsolatot eredményez a Bell kettős és Stirling második számú polinommal,

(21)

Dobiński képlete.Ezért

			(22)
			(23)
			(24)

A központi mozzanatokat ezután kiszámíthatjuk

			(25)
			(26)
			(27)

div id = “da737dd956″>