Mérés: Képletek felfedezése területhez

Területképletek

Azok a hallgatók, akiknek informális felfogása szerint a terület a “2-D mennyiség” Egy régióban található „cuccok” kitalálhatják maguknak a képletek nagy részét, amelyeket gyakran csupán memorizálásra kérnek tőlük. Minden általuk feltalált képlet segít megértésük (és memóriájuk) megerősítésében a többi általuk ismert képlettel kapcsolatban. (Lásd még a felületet.)

Téglalapok területe

Ha négyzetet választunk területegységnek, intuitív képet kapunk a téglalapok területéről. Ha úgy döntünk, hogy ennek a négyzetnek a területe 1, akkor egy hétszer hosszabb téglalap 7 × 1 mint a területe.

A kétszeres magasságú téglalap területe kétszerese, tehát a 2 × 7 területegység. Megszámolhatjuk a négy négyzet két sorát. Hasonlóképpen, a -nek 3 sora van 7 négyzetből (vagy 7 oszlop 3 négyzetből), összesen 7 × 3 négyzetből, tehát területe 21 négyzetegység.

Az egy sorban lévő négyzetek száma a téglalap hossza. A sorok száma a téglalap magassága. Tehát a terület hossza × magassága.

Mivel egy téglalapot ferdén lehet megrajzolni, a „magasság” azt jelenti, hogy „az alapra merőleges irányt” jelenti, és az „alapot” a nos, akármelyik oldalt is választja.

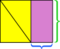
Ez a számok számlálásához, sőt a frakciókhoz is alkalmas. 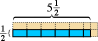Az itt látható kék téglalap a felét méri Ha a megfelelő egység négyzetet választjuk területegységnek, akkor azt látjuk, hogy a kék téglalap öt fél egységnyi területet és egy negyed egységnyi területet tartalmaz, vagy összesen két és háromnegyed egységnyi terület. (A rózsaszínű részek az egyes négyzet alakú területegységek kitöltését mutatják.)

Az összes szám felvétele érdekében meghatározzuk a téglalap területét alap × magasság (ahol az “alap” és a “magasság” az oldalak hosszát jelenti, ugyanazokban az egységekben mérve).

A paralelogrammák területe

Az ötlet megszerzése

Kiszámíthatjuk a paralelogramma területének képletét boncolással a paralelogrammát és az alkatrészeket átrendezve téglalap alakúra. Mivel a paralelogramma és a téglalap ugyanazokból a részekből áll, szükségszerűen azonos területűek. (További információ arról, hogy miért ugyanazok a területek, lásd a terület definícióját.)

Láthatjuk, hogy nekik is vannak pontosan ugyanaz az alaphossz (kék) és pontosan ugyanolyan magasságú (zöld). Mivel az alap × magasság megadja a téglalap területét, ugyanazokat a méréseket használhatjuk a paralelogrammán annak területének kiszámításához: alap × magasság. (A korábbiakhoz hasonlóan a “magasságot” merőlegesen mérjük az aljzatra, és az “alap” az első oldalra választott oldalt választja. Lásd a paralelogrammát.)

A fent látható vágás segítségével könnyen belátható, hogy az alap hossza változatlan. Valójában a merőleges vágás bárhol elvégezhető az alap mentén.

A lyukak felemelése

Intuíció és bizonyítás

Ez a boncolás intuitív megértést ad a paralelogramma területképletéről, és ennek oka annak, hogy annak legyen, ami. De nem kérdőjeleztük meg, hogy a boncolás valóban “működik-e”. Vagyis amikor elvágjuk a paralelogrammát és átrendezzük annak részeit, akkor várhatóan lesz, és az eredmény minden bizonnyal így néz ki. a látszat csalóka lehet. Mi biztosít minket arról, hogy amikor a háromszöget elmozdítjuk, az eredmény egy téglalap lesz? Mi van, ha inkább -re hasonlít (bár kevésbé túlzó)? Ha az eredmény nem mindig tökéletes téglalap, nem használhatjuk a téglalap területi képletének ismereteit a paralelogramma képletének kidolgozására. A középiskolában a diákok képesek lesznek bizonyítani, hogy a paralelogramma két része, ha megfelelően összerakják, téglalapot alkot . A K-8 évfolyamon a hallgatóknak többnyire a vizuális kísérletre kell támaszkodniuk, és intuitív érzetet kell szerezniük. Tudjon meg többet arról, miért működnek ezek a boncolgatások. div> Mi van, ha a rövid oldalt választjuk alapnak?

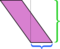
Bármelyik oldalt szabadon választhatjuk alapnak; “magasság” meghatározása szerint merőlegesen mérve arra az oldalra, amelyet alapnak választunk. Ha a rövid oldalt (kék) vesszük alapul, a fent bemutatott boncolás nem olyan meggyőző. A magasság vágása és az alkatrészek átrendezése rendetlenséget okoz:

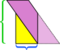
Ebben a példában meg tudjuk menteni a rendetlenséget egy újabb vágással, 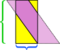, de mi lenne, ha a paralelogramma még hosszabb és soványabb lenne?

Kiderült, hogy bármilyen paralelogramma, függetlenül attól, hogy hosszú és sovány, ilyen módon bontható fel, így a részek – talán sokuk is – téglalap alakúra rendezhetők. De több munka kell annak kimutatásához, hogy ez mindig megtehető. Szükségünk van egy másik ötletre.

Egy kissé eltérő boncolási ötlet ebben az esetben sokkal megkönnyíti az életet. (Önállóan megmutathatja, hogy az eredeti esetben is működik.)

• Zárja be a paralelogrammát egy téglalapba.
• A téglalap két része, amely nincs a paralelogrammán belül, egybevágó háromszög.
• Csúsztassa e háromszögek egyikét a másik felé, amíg össze nem ütköznek, és téglalapot alkotnak. Mivel a külső téglalap teljes területe nem változott (ugyanaz a téglalap, mint korábban), és a sárga terület sem változott (a darabok éppen csak mozogtak). nekik – a lila területeknek – azonosaknak kell lenniük. Az előzőekhez hasonlóan azt is láthatjuk, hogy a téglalap alakú lila terület mérete az eredeti paralelogramma alapja és magassága.

Intuíció és bizonyítás, újból kelés : Ismét a boncolás nyújtja a lényegi betekintést, de egy kicsit több munkát igényel annak biztosítása, hogy a két sárga háromszög, amelyek minden bizonnyal úgy néznek ki, mintha egy négyszög kialakításához illeszkednének egymáshoz, valóban pontosan illeszkednek, és nem csak. p>

Miért fontos ilyen körültekintőnek lenni?

Amikor más területképleteket építünk (alább), akkor arra kell gondolnunk, hogy miként keressük meg a paralelogramma területét, és ezért szeretnénk hogy támaszkodhassunk a megtalált szabályra. Biztosak lehetünk abban, hogy az alkatrészek átrendezése nem változtatja meg a területet: vagyis végül is hogyan határozzuk meg a területet. De abban is biztosnak kell lennünk, hogy az alkatrészek úgy illeszkednek egymáshoz, ahogyan állítjuk, vagy nem támaszkodhatunk az elvégzett mérésekre. És biztosnak kell lennünk abban, hogy az alap × magasság szabály nem függ az alap szerencsés megválasztásától.

A legtöbb tantervben a hallgatóknak nincs elég szisztematikus geometriai alapja a 8. évfolyam előtt, hangos bizonyíték arra, hogy ezek a boncolások működnek. De az intuitív megértés elegendő a képletek magyarázatához és igazolásához, és jó alapok a későbbi geometriai vizsgálatokhoz.

Háromszög területe

A paralelogramma területének megtalálásának ismerete segít keresse meg a háromszög területét.

A háromszög feldarabolása

A háromszöget két részre bonthatjuk – egyikük háromszög, egyikük trapéz – párhuzamos szeleteléssel a bázishoz. Ha ezzel a szelettel pontosan kettévágjuk a magasságot, akkor a két rész egymáshoz illeszkedve azonos alapú, de fele magasságú paralelogrammát képez.

Tehát az alap × félmagasság megadja a háromszög területét. Hasonló boncolás mutatja a fél alap × magasságot. Bármelyikük bh-ra redukálódik.

A háromszög megkétszerezése, majd az így kapott terület felére csökkentése

Egy másik gondolkodásmód: a a háromszög egy paralelogrammát készít, amelynek alapja és magassága megegyezik a háromszögével.

A paralelogramma területe alap × magasság, de ez a kétszerese a háromszög területének, tehát a háromszög területe az alap × magasság, amint azt a boncolási módszerrel láttuk.

(Mint mindig , válasszon egy “alapot”, és mérje meg az alapra merőleges magasságot, az aljától a szemközti csúcsig.)

A trapéz területe

A trapéz megkétszerezése, majd az így kapott terület felezése

Amint az a háromszög esetében igaz volt, a trapéz két példánya egymásba illeszthető egy paralelogramma elkészítéséhez.

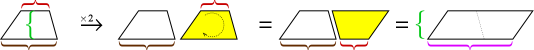
A paralelogramma magassága megegyezik a trapéz magasságával, de az alapja a trapéz két alapjának összege. Tehát a paralelogramma területe magasság × (alap1 + alap2). De ez a terület két trapéz, ezért félbe kell vágnunk, hogy megkapjuk a trapéz területét.

A trapéz feldarabolása

A trapézot is boncolgathatnánk, ahogyan boncoltuk a háromszög, egyetlen szelettel kettévágva a magasságát. A két rész egymással illeszkedve olyan paralelogrammát állít elő, amelynek alapja a trapéz két alapjának összege, de magassága a trapéz magasságának fele.

A trapéz esetében az alapok nem tudnak tetszés szerint választhatók. A két párhuzamos oldal az alap, és a magasság, mint mindig, az egyik alaptól az ellenkezőig merőleges távolság.

A paralelogramma területe a magassága (a trapéz magasságának félmagassága) és az alapja (a trapéz alapjainak összege) szorosa, tehát területe félmagasság × (alap1 + alap2). Mivel a paralelogramma pontosan ugyanabból a “cuccból” készül, mint a trapéz, ezért ez a trapéz területe is.

A trapéz területe mindkét esetben × magasság × (alap1 + alap2).

Egyéb speciális négyszögek területe

A rombusz területe

A rombusz területe megtalálható a darabok vágásával és átrendezésével, hogy ezzel párhuzamos legyen. Ezt többféleképpen lehet megtenni:

1. Vágja át a rövidebb átlót (a), hogy két egybevágó háromszöget alakítson ki. Mozgassa a háromszög alsó felét a felső fele mellett, és ezzel párhuzamos képet képezzen. A rövidebb átló (a) a paralelogramma alapjává, a hosszabb átló (b) fele a paralelogramma magasságává válik. Így a rombusz területe * * div id = “2968ffa1ff”> b vagy az átló szorzata, amely a rombusz standard képlete.
2. Egy másik hasonló módszer az, ha a rombust négy egybevágó háromszögre vágjuk, és átrendezzük egy téglalapra, amelynek alapja a rövidebb átló, a magassága pedig a fele a hosszabb átlónak. a rombust két egybevágó háromszögre, kiszámíthatjuk az egyik háromszög területét, amely * alap (a) * magasság ( b) = ab. Ezután szorozza meg kettővel, mivel kettő van: 2 * ab = ab.

A sárkány területe

A sárkány területe hasonló a rombusz területéhez. A hosszabb átló átmetszése két egybevágó háromszöget eredményez. Ha átrendezzük őket, kialakíthatunk egy paralelogrammát, amelynek alapja a hosszabb átló (b), magassága pedig a rövidebb átló (a) fele. Tehát a terület b * a = ab lesz. A bonyolultabb megközelítés magában foglal egy kis algebrát. Vágja át a sárkányt a rövidebb átlón, hogy két háromszöget kapjon, amelyek alapja a rövidebb átló (a). Így az első háromszög területe a * squiggly, ahol squiggly a magasság. A második háromszög területe a * (b – gubancos), ahol (b – gubancos) a hosszabb átló maradék része. A teljes terület így ( a * squiggly) + ( a * (b – squiggly)) lesz. A a kiszámításakor a (squiggly + b – squiggly) = ab.

Nos, mit tudsz. Alapvetően csak a paralelogramma területének képletét kell ismernie, majd levezetnie a többiek képletét.