Főiskolai algebra (Magyar)
A racionális függvény grafikonjának megnézésével megvizsgálhatjuk lokális viselkedését, és könnyen megnézhetjük, hogy vannak-e aszimptoták. Lehet, hogy közelíteni is tudjuk a helyüket. A grafikon nélkül is meg tudjuk állapítani, hogy van-e egy adott racionális függvénynek aszimptotája, és kiszámíthatjuk azok helyét.
Függőleges aszimptoták
A racionális függvény függőleges aszimptotái lehetnek a nevező azon tényezőinek vizsgálatával találták meg, amelyek nem közösek a számláló tényezőinél. A függőleges aszimptoták az ilyen tényezők nulláinál fordulnak elő.
Hogyan: Ha racionális függvényt kapunk, azonosítsuk a gráfjának függőleges aszimptotáit. nevező.
Kivehető folytonosságok
Esetenként a grafikon tartalmaz egy lyukat: egyetlen pontot, ahol a grafikon nincs meghatározva, jelzi nyitott kör. Ezt a lyukat eltávolítható folytonosságnak hívjuk.
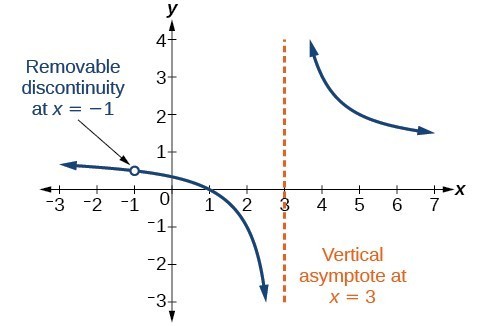
10. ábra
Általános megjegyzés: A racionális függvények eltávolítható folytonosságai
A racionális függvény grafikonján eltávolítható folytonosság lép fel az x = a értéknél, ha a nulla a nevező egy olyan tényezőjénél, amely közös a számláló tényezőjével. Faktorozzuk a számlálót és a nevezőt, és ellenőrizzük a közös tényezőket. Ha találunk ilyet, akkor a közös tényezőt 0-ra állítjuk, és megoldjuk. Ez az eltávolítható folytonosság helye. Ez akkor igaz, ha ennek a tényezőnek a sokasága nagyobb vagy egyenlő a nevezőben szereplővel. Ha ennek a tényezőnek a sokasága nagyobb a nevezőben, akkor továbbra is van egy aszimptota ezen az értéken.
Vízszintes aszimptoták
Míg a függőleges aszimptoták leírják a Ha a kimenet nagyon nagy vagy nagyon kicsi lesz, a vízszintes aszimptoták segítenek leírni a gráf viselkedését, mivel a bemenet nagyon nagy vagy nagyon kicsi. Emlékezzünk vissza arra, hogy a polinom végső viselkedése tükrözi a vezető kifejezés viselkedését. Hasonlóképpen, a racionális függvény végső viselkedése tükrözi a számláló és a nevező függvények vezető kifejezéseinek arányát.
A vízszintes aszimptoták ellenőrzésénél három különböző eredmény van:
Eset 1: Ha a nevező mértéke > a számláló fokozata, akkor az y = 0-nál vízszintes aszimptota van.

2. eset: Ha a számláló nevezőjének mértéke < a számláló fokozata egy, akkor ferde aszimptotát kapunk.

Vegyük észre, hogy bár egy racionális függvény grafikonja soha nem fog keresztezni egy függőleges aszimptotát, a a grafikon keresztezhet vagy nem keresztezhet vízszintes vagy ferde aszimptota. Ezenkívül bár egy racionális függvény grafikonjának sok függőleges aszimptotája lehet, a grafikonnak legfeljebb egy vízszintes (vagy ferde) aszimptotája lesz.
Meg kell jegyezni, hogy ha a számláló foka nagyobb mint a nevező mértéke egynél több, a grafikon végi viselkedése utánozza a csökkent vég-viselkedési frakció viselkedését. Például, ha megvolt a
végződéssel
a grafikon végső viselkedése hasonló lenne egy egyenletes polinomhoz, pozitív pozitív együtthatóval.
A Általános megjegyzés: Vízszintes Racionális függvények
A racionális függvény vízszintes aszimptotája meghatározható a számláló és a nevező fokozatainak megtekintésével.
- A számláló foka kisebb, mint a nevező foka: vízszintes aszimptota az y = 0-nál.
- A számláló foka eggyel nagyobb, mint a nevező foka: nincs vízszintes aszimptota; ferde aszimptota.
- A számláló foka megegyezik a nevező fokával: vízszintes aszimptota a vezető együtthatók arányában.
Általános megjegyzés: A racionális függvények elfogása
A racionális függvénynek y-metszete lesz, ha a bemenet nulla, ha a függvény nullán van meghatározva. A racionális függvénynek nincs y-metszete, ha a függvény nincs nullán definiálva.
Hasonlóképpen, a racionális függvénynek x-metszete lesz a bemeneteknél, amelyek a kimenetet nullára teszik. Mivel a törtrész csak akkor nulla, ha a számláló nulla, az x-lehallgatások csak akkor fordulhatnak elő, ha a racionális függvény számlálója nulla.
Próbálja ki 7
Ha a reciprok négyzet függvényt 3 egységgel jobbra és 4 egységet lefelé toljuk, írjuk ezt racionális függvényként. Ezután keresse meg az x– és y metszeteket, valamint a vízszintes és függőleges aszimptotákat.
Megoldás