Exponenciális eloszlás
, PhD Marco Taboga
Az exponenciális eloszlás folyamatos valószínűségi eloszlás, amelyet modellezzük azt az időt, amelyre várnunk kell, mielőtt egy adott esemény bekövetkezne. Ez a geometriai eloszlás folyamatos megfelelője, amely inkább diszkrét.
Néha negatív exponenciális eloszlásnak is nevezik.
Bevezetés
Mennyi idő telik el egy földrengésig egy adott régióban? Mennyi ideig kell várni, amíg egy vásárló belép az üzletünkbe? Mennyi időbe telik, amíg a telefonközpont fogadja a következő telefonhívást? Mennyi ideig fog működni egy gép anélkül, hogy elromlana?
Az ilyen kérdésekre gyakran valószínűségi fogalmakkal válaszolunk az exponenciális eloszlás használatával.
Mindezek a kérdések a szükséges időre vonatkoznak. várni, amíg egy adott esemény bekövetkezik. Ha ez a várakozási idő ismeretlen, gyakran célszerű véletlen változónak gondolni, amelynek exponenciális eloszlása van.
Nagyjából szólva a 
időre van szükségünk várni egy esemény bekövetkezése előtt exponenciális eloszlású, ha annak valószínűsége, hogy az esemény egy bizonyos időintervallumban bekövetkezik, arányos az adott időintervallum hosszával.
Pontosabban: nak exponenciális eloszlása van, ha a feltételes valószínűség hozzávetőlegesen arányos az idők közötti időintervallum hosszával és , bármikor .
Sok gyakorlati helyzetben ez a tulajdonság nagyon reális. Ez az oka annak, hogy az exponenciális eloszlást olyan széles körben használják a várakozási idők modellezésére.
Az exponenciális eloszlás szigorúan összefügg a Poisson-eloszlással. Ha 1) egy esemény többször is előfordulhat, és 2) a két egymást követő esemény között eltelt idő exponenciálisan oszlik el és független a korábbi eseményektől, akkor az esemény egy adott időegységen belüli előfordulásainak száma Poisson-eloszlású. Felhívjuk az olvasót, hogy olvassa el a Poisson-disztribúcióról szóló előadást, amely részletesebb magyarázatot és intuitív grafikus ábrázolást tartalmaz erről a tényről. / p>
Definíció Legyen folyamatos véletlen változó. Támogatása legyen a pozitív valós számok halmaza: Legyen . Azt mondjuk, hogy a exponenciális eloszlás paraméterrel rendelkezik, csak akkor, ha annak valószínűségi sűrűségfüggvénye
Aparamétert hívják sebességparaméternek.
Az exponenciális eloszlású véletlen változót exponenciális véletlen változónak is nevezzük.
A következő bizonyíték arra, hogy egy legitim valószínűségi sűrűségfüggvény.
A nem negativitás nyilvánvaló. Bizonyítanunk kell, hogy a integrálja a fölött megegyezik a értékkel. Ezt a következőképpen bizonyítják:
Az exponenciális eloszlás jobb megértése érdekében megnézheti annak sűrűségi ábráit.
A ráta paraméter és értelmezése
Említettük, hogy annak valószínűsége, hogy az esemény két dátum és arányos a következővel: (attól az információtól függ, hogy előtt nem történt-e meg). A sebességparaméter az arányosság állandója: ahol végtelen kicsi magasabb rendű, mint a (azaz a függvény, amely gyorsabban nullázódik, mint a igen).
A fenti arányossági feltétel is elegendő az exponenciális eloszlás teljes jellemzéséhez.
Tétel: Az arányosság feltétele csak akkor teljesül, ha a exponenciális eloszlású.
A feltételes valószínűség a következővel írható: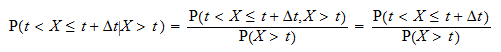 
Jelölje kifejezéssel az elosztási függvényét, vagyis és túlélési funkciója: Ezután Mindkét oldalt elosztva , megkapjuk ahol egy olyan mennyiség, amely amikor . Mindkét oldalon korlátokat véve -t vagy a derivált definíciója szerint: Ezt a differenciálegyenletet könnyen meg lehet oldani a lánc használatával szabály: Ha az integrált -ből mindkét oldal -be vesszük, akkor és vagy De (mivel nem vehet fel negatív értékeket) azt jelenti, hogy Mindkét oldalt hatványozva Ezért vagy De a sűrűségfüggvény az elosztási függvény első származéka: és a jobb szélső tag egy exponenciális véletlen változó sűrűsége. Ezért az arányossági feltétel csak akkor teljesül, ha a exponenciális véletlen változó
Várható érték
Egy exponenciális véletlen változó várható értéke
Az alábbiak szerint vezethető le: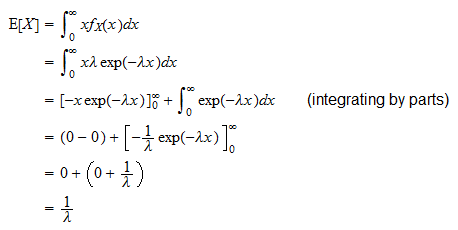 
Variancia
Egy exponenciális véletlen változó
Ez levezethető a szokásos varianciaképletnek (): 
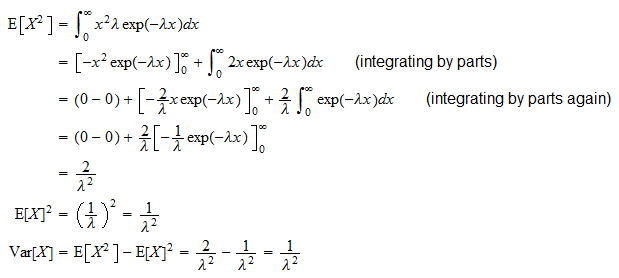
Pillanatgeneráló függvény
Egy exponenciális véletlen változó pillanatgeneráló függvénye minden :
A pillanatgeneráló függvény meghatározása természetesen a fenti integrálok csak akkor konvergálnak, ha , azaz csak akkor, ha . Ezért minden esetén létezik egy exponenciális véletlen változó pillanatgeneráló függvénye.
Jellemző függvény
A exponenciális véletlen változó jellemző funkciója
A karakterisztikus függvény definíciójának és annak a ténynek a felhasználásával, hogy írhatunk . Az első integrál a 
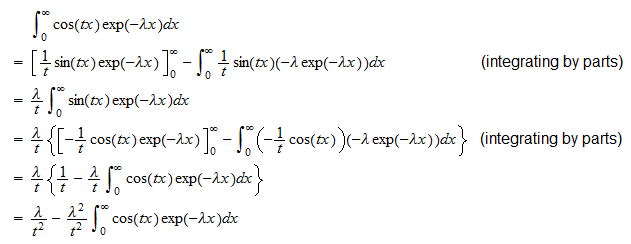Ezért , amely átrendezhető vagy A második integrál 
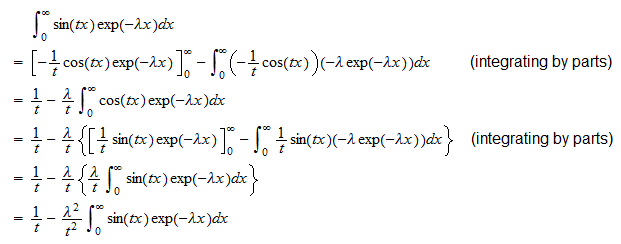Ezért , amely átrendezhető a vagy A darabok összerakásával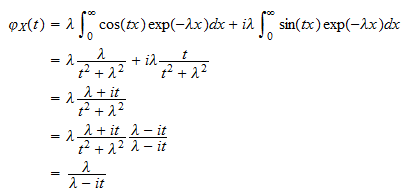 
Terjesztési függvény
Egy exponenciális véletlen változó elosztási függvénye
Ha , akkor mert nem vehet fel negatív értékeket. Ha , akkor
További részletek
A következő alfejezetekben további részleteket találhat az exponenciális eloszlásról.
Memória nélküli tulajdonság
Az exponenciális eloszlás egyik legfontosabb tulajdonsága a memória nélküli tulajdonság: bármely esetén.
Ezt a következőképpen bizonyítják: A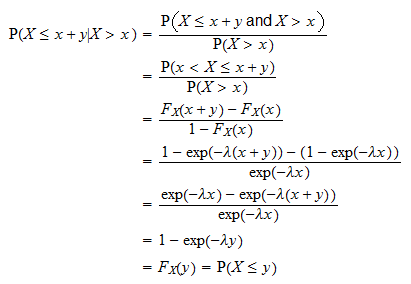 
az az idő, amelyet várnunk kell egy bizonyos esemény előtt bekövetkezik. A fenti tulajdonság azt mondja, hogy annak valószínűsége, hogy az esemény egy hosszúságú intervallum alatt történik, független attól, hogy mennyi idő telt el () anélkül, hogy az esemény bekövetkezne.
Az exponenciális véletlen változók összege egy Gamma véletlen változó
Tegyük fel, hogy , , …, kölcsönösen független, exponenciális eloszlású, véletlen változók paraméterrel.
Define
Ezután az összeg egy Gamma véletlen változó, paraméterei és .
Ezt a pillanat segítségével bizonyítják generáló függvények (ne feledjük, hogy a kölcsönösen független véletlen változók összegének pillanatgeneráló függvénye csak a pillanatgeneráló függvényeik szorzata): Ez utóbbi egy Gamma pillanatgeneráló függvénye terjesztés paraméterekkel és . Tehát a Gamma eloszlású, mert két véletlen változónak ugyanaz az eloszlása, ha ugyanazon pillanatgeneráló funkcióval rendelkeznek.
Az véletlen változóról néha azt is mondják, hogy Erlang eloszlású. Az Erlang eloszlás csak egy speciális esete a Gamma eloszlásnak: a Gamma véletlen változó akkor is Erlang véletlen változó, ha exponenciális véletlen változók összegeként írható fel.
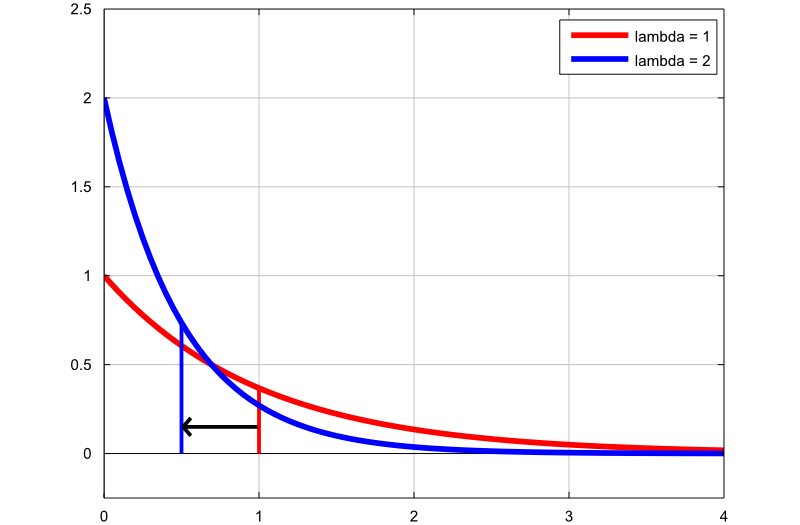
Sűrűségdiagram
A következő ábra bemutatja, hogyan változik az exponenciális eloszlás sűrűsége a sebességparaméter megváltoztatásával:
-
az első gráf (piros vonal) egy exponenciális véletlen változó valószínűségi sűrűségfüggvénye
sebességparaméterrel; -
a második grafikon (kék vonal) egy exponenciális véletlen változó valószínűségi sűrűségfüggvénye
paraméterrel.
A vékony függőleges vonalak jelzik a két eloszlás átlagát. Vegye figyelembe, hogy a sebességparaméter növelésével csökkentjük az eloszlás átlagát -ről -re.
Megoldott gyakorlatok
Az alábbiakban néhány gyakorlatot talál, magyarázattal megoldva.
1. gyakorlat
Legyen exponenciális véletlen változó a paraméterrel. Számítsa ki a következő valószínűséget:
A valószínűséget először felhasználva azt a tényt, hogy annak a valószínűsége, hogy egy folytonos véletlenszerű változó bármely meghatározott értéket felvesz, egyenlő nulla (lásd Folyamatos véletlen változók és nulla valószínűségű események). Most a valószínűség a elosztási függvényében írható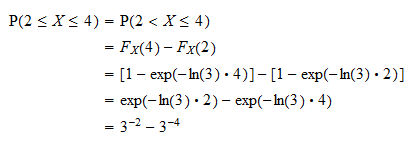 
2. gyakorlat
Tegyük fel, hogy a véletlen változónak van egy exponenciális eloszlása a paraméterrel. Számítsa ki a következő valószínűséget:
Ez a valószínűség könnyen kiszámítható a :
3. gyakorlat
Mennyi a valószínűsége annak, hogy egy véletlen változó A értéke kisebb, mint a várt értéke, ha a exponenciális eloszlású paraméterrel ?
A paraméterrel rendelkező exponenciális véletlen változó várható értéke A fenti valószínűség kiszámítható a : elosztási függvény használatával:
Idézés
Kérjük, idézze meg: