BFS vs DFS: Ismerje meg a különbséget

Mi a BFS ?

A BFS egy algoritmus, amelyet adatok ábrázolására, fák keresésére vagy áthaladó struktúrákra használnak. Az algoritmus hatékonyan meglátogatja és megjelöli az összes kulcscsomópontot egy grafikonon, pontosan szélességben.

Ez az algoritmus egyetlen csomópontot (kezdeti vagy forráspontot) választ ki a grafikonból, majd meglátogatja a kiválasztott csomópont melletti összes csomópontot. Amint az algoritmus meglátogatja és megjelöli a kezdő csomópontot, akkor a legközelebbi nem látogatott csomópontok felé halad és elemzi őket.

Miután meglátogatta az összes csomópontot megjelöli. Ezek az iterációk addig folytatódnak, amíg a grafikon összes csomópontját sikeresen meg nem látogatták és meg nem jelölte. A BFS teljes formája a Szélesség első keresése.

Ebben a BSF Vs. DFS bináris fa oktatóanyag, megtanulja:

• Mi az a BFS?
• Mi az a DFS?
• Példa BFS-re
• Példa DFS-re
• Különbség a BFS és a DFS bináris fa között
• A BFS alkalmazásai
• A DFS alkalmazásai

Mi az az DFS?

A DFS egy algoritmus, amellyel grafikonokat vagy fákat találhatunk vagy haladhatunk át mélységirányban. Az algoritmus végrehajtása a gyökércsomópontnál kezdődik, és az egyes ágakat feltárja, mielőtt visszalép. Verem adatstruktúrát használ az emlékezésre, a későbbi csúcs megszerzésére és a keresés indítására, valahányszor zsákutca jelenik meg bármely iterációban. A DFS teljes formája a Mélység-első keresés.

Példa a BFS-re

A DFS következő példájában 6 csúcsú gráfot használtak.

Példa a BFS-re

1. lépés)

Hét számgrafikonja van, 0 és 6 között.

2. lépés)

0 vagy nullát jelöltünk meg gyökércsomópontként.

3. lépés)

0 meglátogatott, megjelölt , és beillesztette a sor adatstruktúrájába.

4. lépés)

0 szomszédos és meg nem látogatott marad a csomópontokat meglátogatják, megjelölik és beillesztik a sorba.

5. lépés)

Az áthaladó iterációkat mindaddig ismételjük az összes csomópont meglátogatott.

DFS példa

A következő DFS példában irányítatlan, 5 csúcsú gráfot használtunk.

1. lépés:

A 0. csúcsból indultunk. Az algoritmus azzal kezdődik, hogy felkeresi a meglátogatott listába, és az összes szomszédos csúcsát egyidejűleg az adatokba helyezi veremnek nevezett szerkezet.

2. lépés)

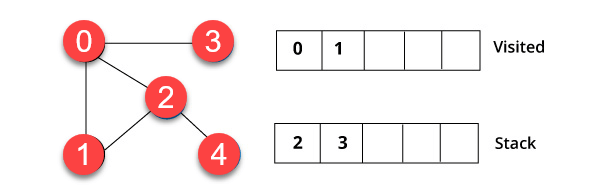
Meglátogatja az elemet , amely például a verem tetején található, 1 és menjen a szomszédos csomópontokhoz. Ez azért van, mert a 0 már meglátogatott. Ezért meglátogatjuk a 2. csúcsot.

3. lépés)

Vertex 2 nem látogatott közeli csúcsa a 4-ben található. Ezért hozzáadjuk ezt a veremhez, és meglátogatjuk.

4. lépés)

Végül meglátogatjuk az utolsó 3 csúcsnak nincsenek meglátogatatlan szomszédos csomópontjai. A grafikon áthaladását DFS algoritmus segítségével fejeztük be.

Különbség a BFS és az DFS bináris fa között

A

BFS	DFS
A BFS megtalálja a legrövidebb utat a célig.	A DFS egy alfa aljára megy, majd visszalép .
A BFS teljes formája a Breadth-First Search.	A DFS teljes formája a Depth First Search.
Várakozási sorral követi nyomon a következő felkeresendő helyet.	Verem segítségével nyomon követheti a következő meglátogatott helyet.
A BFS a fa szintje szerint halad.	A DFS a fa mélysége szerint halad.
FI használatával valósul meg. FO lista.	A LIFO lista segítségével valósítják meg.
A DFS-hez képest több memóriára van szükség.	Kevesebb memóriát igényel, mint a BFS-ben.
Ez az algoritmus adja a leg sekélyebb út megoldást.	Ez az algoritmus nem garantálja a leg sekélyebb út megoldását.
A BFS-ben nincs szükség visszalépésre.	Van visszakövetés szükségessége a DFS-ben.
Soha nem lehet véges hurkokba csapdába esni.	Végtelen hurkokba csapdába eshet.
Ha nem talál semmilyen célt, akkor sok csomópontot ki kell bővítenie a megoldás megtalálása előtt.	Ha nem talál célt, a levélcsomópont visszakövetése előfordul.

A BFS alkalmazásai

Itt vannak a BFS alkalmazásai:

Súlyozatlan Grafikonok:

A BFS algoritmus könnyen létrehozhatja a legrövidebb utat és egy minimális átfedő fát, hogy a grafikon összes csúcsát a lehető legrövidebb idő alatt, nagy pontossággal látogassa meg.

P2P hálózatok:

A BFS megvalósítható az összes legközelebbi vagy szomszédos csomópont megkeresésére a peer to peer hálózatban. Ez gyorsabban megtalálja a szükséges adatokat.

Webrobotok:

A keresőmotorok vagy a webrobotok könnyen létrehozhatnak többszintű indexeket BFS alkalmazásával. A BFS megvalósítása a forrásból indul ki, amely a weboldal, majd meglátogatja az adott forrás összes hivatkozását.

Hálózati műsorszórás:

A BFS algoritmus vezérli a sugárzott csomagokat az összes csomópont megtalálásához és eléréséhez.

Az DFS alkalmazásai

Íme a DFS fontos alkalmazásai:

Súlyozott grafikon:

Súlyozott gráfban az DFS gráf átjárása generál a legrövidebb útfa és a legkisebb átívelő fa.

Ciklus észlelése a grafikonon:

A grafikonnak van ciklusa, ha a DFS során hátsó élt találtunk. Ezért futtatnunk kell a grafikus DFS-t, és ellenőriznünk kell a hátsó éleket.

Útkeresés:

A DFS algoritmusra szakosodhatunk utat keresni két csúcs között.

Topológiai rendezés:

Elsősorban a feladatok ütemezésére szolgál az adott függőségektől a munkacsoport között. A számítástechnikában az utasítások ütemezésében, az adatok sorosításában, a logikai szintézisben, a fordítási feladatok sorrendjének meghatározásában használják.

Grafikon erősen összekapcsolt komponenseinek keresése:

A DFS-grafikonban akkor használja, ha a grafikon minden egyes csúcsától a többi megmaradt csúcsig van útvonal.

Rejtvények megoldása csak egy megoldással:

A DFS algoritmus könnyen adaptálható az útvesztő összes megoldásának keresésére azáltal, hogy csomópontokat tartalmaz a meglévő útvonalon a meglátogatott készletben.