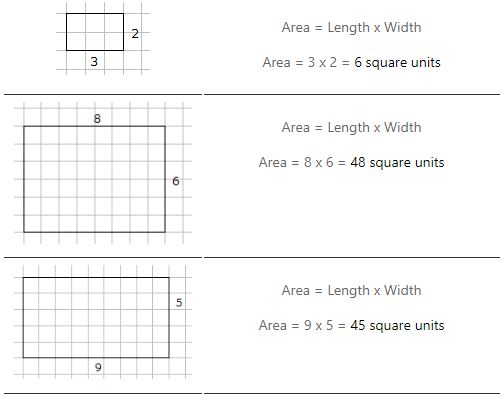
A terület kiszámítása
A terület kiszámítása
A területet négyzetben (vagy négyzetegységben) mérjük.
Hány négyzet van ebben a téglalapban?

Megszámolhatjuk a négyzeteket, vagy megtehetjük vegye be a hosszúságot és a szélességet, és használja a szorzást. A fenti téglalap területe 15 négyzetegység.
A téglalap területe = hossz x szélesség
Példák egy téglalap területének kiszámítására
Egységek a terület méréséhez
Területet mérünk négyzetek segítségével. Különböző méretű négyzeteket használunk, attól függően, hogy mekkora vagy kicsi a terület.
| Példa | Négyzetek oldalának hossza | Egység |
| A méret szegezd a hüvelykujjadra | milliméter | mm2 |
| A papír mérete | centiméter | cm2 |
| A szoba mérete | Mérő | m2 |
| A város mérete | Kilométer | km2 |
Ne felejtsd el a picikét
Négyzetméreteket írunk az egység melletti kis 2-vel.
mm2, cm2, m2, km2, cm2 értéket írunk
Mondhatjuk “63 milliméter négyzetben” vagy “63 négyzet milliméter”
Kis négyzetekkel mérhetnénk nagy területeket. Az egyetlen probléma ezzel az, hogy a végén nagyon nagyokat kell használnunk számok. Például egy mezőt 5 000 000 000 négyzetmilliméterre lehet mérni, amikor 5000 négyzetméter sokkal könnyebb méretet mondani, írni és megjeleníteni.
Valószínűleg több egységet fog hallani a terület mérésére; négyzethüvelyk, négyzetláb, négyzetméter, négyzetmérföld, hektár, hektár az egység, amelyet a terület mérésére használnak.
További példák a terület kiszámítására
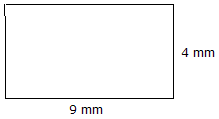 |
Terület = Hossz x Szélesség Terület = 9 mm x 4 mm = 36 mm2 |
 |
Terület = Hossz x Szélesség Terület = 7 cm x 6 cm = 42 cm2 |
 |
Terület = Hossz x Szélesség Terület = 8 mx 2 m = 16 m2 |
 |
Terület = Hossz x Szélesség Terület = 7 km x 5 km = 35 km2 |
Négyzet területe
A négyzet hossza és szélessége megegyezik, ezért csak meg kell szorozni a hosszat a hosszúsággal.
| Terület = Hossz x Hossz Terület = 6 cm x 6 cm = 36 cm2 |
Egy kör területe
A kör területe = πr2
ahol r a kör sugara, π pedig a kör kerületének és az átmérőjének az aránya.
π (ejtsük „pite” -nek és gyakran írjuk „Pi” -nek) egy végtelen tizedesjegy, közös 3,14159 közelítése. Itt többet megtudhat a Pi-ről
Példa egy kör területének kiszámítására
 |
Terület = πr2 Terület = 3,14159 x (4 cm) 2 Terület = 3,14159 x 16 cm2 Terület = 50,27 cm2 Válasz 2 tizedesjegyre kerekítve |
A kör képletének területének magyarázata
Vegyünk egy kört, és osszuk el azonos méretű szektorokra és ezeket az alábbiak szerint rendezze át. Figyelje meg, hogy a szektorok kisebbé válásával az alak inkább téglalap alakúvá válik. Megjegyzés: Nincs korlátozás, hogy ezek a szektorok milyen kicsiek lehetnek, és mennyire hasonlíthatnak egy téglalapra, ha elrendezik őket.
Feltételezve, hogy tudjuk, hogy egy kör kerülete 2πr, akkor hozzáadhatunk dimenziókat a “téglalap” az alábbiak szerint. Egy téglalap alakú terület képletének (terület = szélesség x magasság) használatával láthatjuk, hogy a téglalapként átkonfigurált körünknek hogyan lehet egy olyan területe, amely megközelítőleg πr xr vagy πr2
kör Átrendezett szektorok

Körszektorok átrendezve – indítás téglalapnak nézni

Összetett alakzatok
Sok esetben előfordul, hogy egy teljes terület kiszámításához egynél több területet kell kiszámítani, majd összeadás, kivonás vagy a műveletek valamilyen más kombinációja követi a kívánt terület megtalálását.
Megjegyzés: Az alábbi példákban a mértékegységek nem jelennek meg, és a válaszok, valamint a π (Pi) értéke a legközelebbi századikra kerekítve van.
Az alábbi területszámítási példa viszonylag egyszerű. Az alakzat háromszögnek tekinthető, téglalapgal kombinálva.
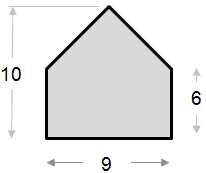 |
A háromszög rész területe: ½ x alap x magasság ½ x 9 x 4 = 18 A téglalap rész területe: Teljes terület = 18 + 54 = 72 |
A fenti példa egy általános követelményt szemléltet, ha összetettel dolgozunk alakzatok – olyan dimenziók keresése, amelyek nem láthatók. Gyermekeinek oktatása során szükség esetén segítsen megtalálni ezeket a “hiányzó” dimenziókat. Az alábbiakban található egy másik példa.
A dimenziók megkeresése
 |
Milyen méretűek a kis téglalap alakú részek? Szélesség? 12 – 7 – 2 = 3 Magasság? 8 – 6 = 2 |
Példa: Az egyik terület kivonása a másikból
Az alábbi példában az alak téglalapként tekinthető kivágott háromszöggel.
 |
A téglalap rész területe: szélesség x magasság 5 x 6 = 30 A háromszög rész területe: Teljes terület = 30 – 4,50 = 25,50 |
Példa: Részterületek
Az alábbi példa hasonló a fentihez, bár mivel félkörünk van, egy töredéket (felét) kell kiszámítanunk a kör területét. Ebben a példában vegye figyelembe az átmérőt, és ne a sugarat.
 |
A háromszög rész területe: ½ x alap x magasság ½ x 6 x 6 = 18 A félkör alakú terület területe: Teljes terület = 18 – 3,53 = 14,47 |
Példa: Döntések! Kombájn? Kivonás
Gyakran előfordul, hogy a végső terület kiszámításához többféle módszer is van. Az alábbi példákban az alakzat két téglalapnak tekinthető, vagy egy nagy téglalapnak, amelynek kisebb téglalapja van “kivágva” a jobb felső sarokból.
Terület munkalapok kiszámítása
Nyomtatás készítse el az alább felsorolt munkalapokat, és használja őket a gyermekek oktatásakor.
- Területek kiszámítása – téglalapok és négyzetek
- Területek kiszámítása – téglalapok
- kiszámítása Területek – téglalapok
- Összetett területek kiszámítása pl téglalap alakú
- Összetett területek kiszámítása pl. téglalapokkal, háromszögekkel és körökkel
- A területek kiszámítása pl. háromszögek
- egy kör területe
- felszíni területek kiszámítása pl. téglalap alakú prizmák
További nyomtatható geometriai munkalapokat itt talál.