Exponentialverteilung
von Marco Taboga, PhD
Die Exponentialverteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung, die verwendet wird Modellieren Sie die Zeit, die wir warten müssen, bevor ein bestimmtes Ereignis eintritt. Es ist das kontinuierliche Gegenstück zur geometrischen Verteilung, die stattdessen diskret ist.
Manchmal wird es auch als negative Exponentialverteilung bezeichnet.

Einführung
Wie viel Zeit wird vergehen, bis ein Erdbeben in einer bestimmten Region auftritt? Wie lange müssen wir warten, bis ein Kunde unseren Shop betritt? Wie lange dauert es, bis ein Callcenter den nächsten Anruf erhält? Wie lange funktioniert eine Maschine ohne Ausfall?
Fragen wie diese werden häufig unter Verwendung der Exponentialverteilung probabilistisch beantwortet.
Alle diese Fragen betreffen die Zeit, die wir benötigen warten, bevor ein bestimmtes Ereignis eintritt. Wenn diese Wartezeit unbekannt ist, ist es oft angebracht, sie als Zufallsvariable mit Exponentialverteilung zu betrachten.
Grob gesagt, die Zeit  , die wir benötigen Warten, bevor ein Ereignis eintritt, hat eine Exponentialverteilung, wenn die Wahrscheinlichkeit, dass das Ereignis während eines bestimmten Zeitintervalls auftritt, proportional zur Länge dieses Zeitintervalls ist.
, die wir benötigen Warten, bevor ein Ereignis eintritt, hat eine Exponentialverteilung, wenn die Wahrscheinlichkeit, dass das Ereignis während eines bestimmten Zeitintervalls auftritt, proportional zur Länge dieses Zeitintervalls ist.
Genauer gesagt,  hat eine Exponentialverteilung, wenn die bedingte Wahrscheinlichkeit
hat eine Exponentialverteilung, wenn die bedingte Wahrscheinlichkeit  ungefähr proportional zur Länge
ungefähr proportional zur Länge  des Zeitintervalls zwischen den Zeiten ist
des Zeitintervalls zwischen den Zeiten ist  und
und  zu jedem Zeitpunkt
zu jedem Zeitpunkt  .
.
In vielen praktischen Situationen ist diese Eigenschaft sehr realistisch. Dies ist der Grund, warum die Exponentialverteilung so häufig zur Modellierung von Wartezeiten verwendet wird.
Die Exponentialverteilung hängt eng mit der Poisson-Verteilung zusammen. Wenn 1) ein Ereignis mehr als einmal auftreten kann und 2) die zwischen zwei aufeinanderfolgenden Ereignissen verstrichene Zeit exponentiell verteilt und unabhängig von früheren Ereignissen ist, hat die Anzahl der Ereignisse des Ereignisses innerhalb einer bestimmten Zeiteinheit eine Poisson-Verteilung. Wir laden den Leser ein, die Vorlesung über die Poisson-Verteilung zu lesen, um eine detailliertere Erklärung und eine intuitive grafische Darstellung dieser Tatsache zu erhalten.
Definition
Die Exponentialverteilung ist wie folgt charakterisiert.
Definition Sei  eine kontinuierliche Zufallsvariable. Die Unterstützung sei die Menge positiver reeller Zahlen:
eine kontinuierliche Zufallsvariable. Die Unterstützung sei die Menge positiver reeller Zahlen:  Sei
Sei  . Wir sagen, dass
. Wir sagen, dass  eine Exponentialverteilung mit dem Parameter
eine Exponentialverteilung mit dem Parameter  hat, wenn und nur wenn seine Wahrscheinlichkeitsdichtefunktion
hat, wenn und nur wenn seine Wahrscheinlichkeitsdichtefunktion  Der Parameter
Der Parameter  wird als Ratenparameter bezeichnet.
wird als Ratenparameter bezeichnet.
Eine Zufallsvariable mit einer Exponentialverteilung wird auch als exponentielle Zufallsvariable bezeichnet.
Das Folgende ist ein Beweis dafür, dass  ist eine legitime Wahrscheinlichkeitsdichtefunktion.
ist eine legitime Wahrscheinlichkeitsdichtefunktion.
Nicht-Negativität ist offensichtlich. Wir müssen beweisen, dass das Integral von  über
über  gleich
gleich  ist. Dies wird wie folgt bewiesen:
ist. Dies wird wie folgt bewiesen: 
Um die Exponentialverteilung besser zu verstehen, können Sie sich die Dichtediagramme ansehen.
Der Ratenparameter und seine Interpretation
Wir haben erwähnt, dass die Wahrscheinlichkeit, dass das Ereignis zwischen zwei Daten auftritt  und
und  ist proportional zu
ist proportional zu  (abhängig von der Information, dass es nicht vor
(abhängig von der Information, dass es nicht vor  aufgetreten ist). Der Ratenparameter
aufgetreten ist). Der Ratenparameter  ist die Proportionalitätskonstante:
ist die Proportionalitätskonstante:  wobei
wobei  ein Infinitesimal von ist höhere Ordnung als
ein Infinitesimal von ist höhere Ordnung als  (dh eine Funktion von
(dh eine Funktion von  , die schneller auf Null geht als
, die schneller auf Null geht als  tut).
tut).
Die obige Proportionalitätsbedingung reicht auch aus, um die Exponentialverteilung vollständig zu charakterisieren.
Satz Die Proportionalitätsbedingung  ist nur erfüllt, wenn
ist nur erfüllt, wenn  eine Exponentialverteilung hat.
eine Exponentialverteilung hat.
Die bedingte Wahrscheinlichkeit  kann als Bezeichnen Sie mit
kann als Bezeichnen Sie mit  die Verteilungsfunktion von
die Verteilungsfunktion von  , dh
, dh  und durch
und durch  seine Überlebensfunktion:
seine Überlebensfunktion:  Dann
Dann  Teilen Sie beide Seiten durch
Teilen Sie beide Seiten durch  erhalten wir
erhalten wir  wobei
wobei  eine Größe ist, die zu
eine Größe ist, die zu  , wenn
, wenn  zu
zu  tendiert. Wenn wir auf beiden Seiten Grenzen setzen, erhalten wir
tendiert. Wenn wir auf beiden Seiten Grenzen setzen, erhalten wir  oder nach der Definition der Ableitung:
oder nach der Definition der Ableitung:  Diese Differentialgleichung lässt sich leicht mithilfe der Kette lösen Regel:
Diese Differentialgleichung lässt sich leicht mithilfe der Kette lösen Regel:  Wenn wir das Integral von
Wenn wir das Integral von  zu
zu  beider Seiten nehmen, erhalten wir
beider Seiten nehmen, erhalten wir  und
und  oder
oder  Aber
Aber  (weil
(weil  keine negativen Werte annehmen kann) impliziert
keine negativen Werte annehmen kann) impliziert  Wenn beide Seiten potenziert werden, erhalten wir
Wenn beide Seiten potenziert werden, erhalten wir  Daher
Daher  oder
oder  Die Dichtefunktion ist jedoch die erste Ableitung der Verteilungsfunktion:
Die Dichtefunktion ist jedoch die erste Ableitung der Verteilungsfunktion:  und der Term ganz rechts ist die Dichte einer exponentiellen Zufallsvariablen. Daher ist die Proportionalitätsbedingung nur erfüllt, wenn
und der Term ganz rechts ist die Dichte einer exponentiellen Zufallsvariablen. Daher ist die Proportionalitätsbedingung nur erfüllt, wenn  eine exponentielle Zufallsvariable ist.
eine exponentielle Zufallsvariable ist.
Erwarteter Wert
Der erwartete Wert einer exponentiellen Zufallsvariablen  ist
ist 
Es kann wie folgt abgeleitet werden: 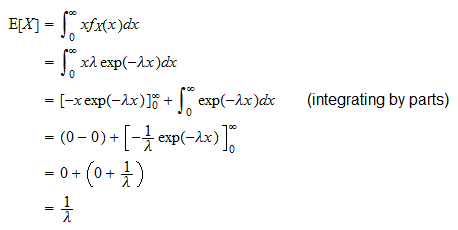
Varianz
Die Varianz von an exponentielle Zufallsvariable  ist
ist 
Es kann dank der üblichen Varianzformel ( ) abgeleitet werden:
) abgeleitet werden: 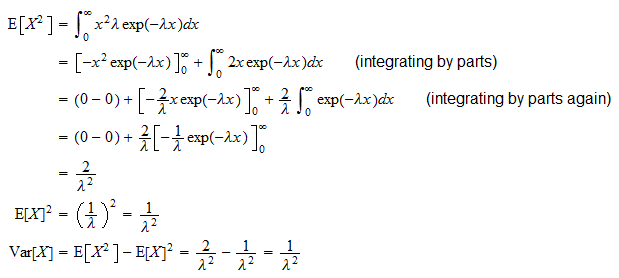
Momenterzeugungsfunktion
Die Momenterzeugungsfunktion einer exponentiellen Zufallsvariablen  ist für jede
ist für jede  definiert:
definiert: 
Die Definition der Momenterzeugungsfunktion ergibt  Von Natürlich konvergieren die obigen Integrale nur, wenn
Von Natürlich konvergieren die obigen Integrale nur, wenn  , d. h. nur wenn
, d. h. nur wenn  . Daher existiert die Momenterzeugungsfunktion einer exponentiellen Zufallsvariablen für alle
. Daher existiert die Momenterzeugungsfunktion einer exponentiellen Zufallsvariablen für alle  .
.
Charakteristische Funktion
Die charakteristische Funktion einer exponentiellen Zufallsvariablen  ist
ist 
Unter Verwendung der Definition der charakteristischen Funktion und der Tatsache, dass  wir schreiben können
wir schreiben können  Berechnen wir nun die beiden Integrale getrennt . Das erste Integral ist
Berechnen wir nun die beiden Integrale getrennt . Das erste Integral ist 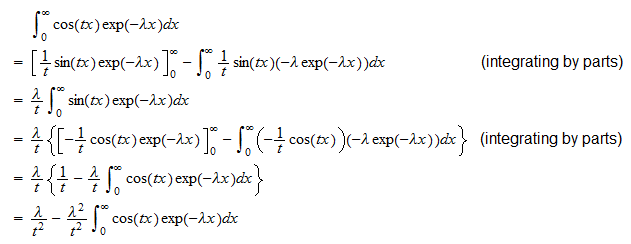 Daher
Daher  , das neu angeordnet werden kann, um
, das neu angeordnet werden kann, um  oder
oder  Das zweite Integral ist
Das zweite Integral ist 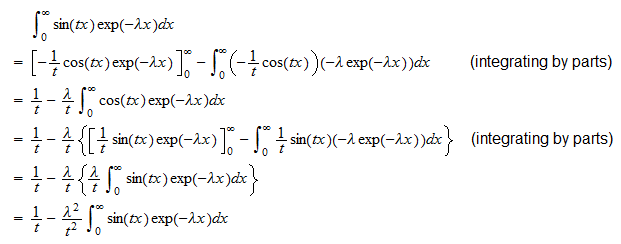 Daher
Daher  , das neu angeordnet werden kann, um
, das neu angeordnet werden kann, um  oder
oder  Durch Zusammenfügen von Teilen erhalten wir
Durch Zusammenfügen von Teilen erhalten wir 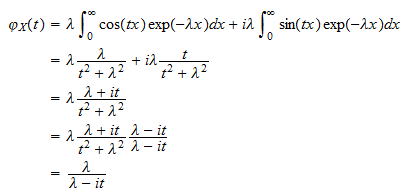
Verteilungsfunktion
Die Verteilungsfunktion einer exponentiellen Zufallsvariablen  ist
ist 
Wenn  , dann
, dann  weil
weil  kann keine negativen Werte annehmen. Wenn
kann keine negativen Werte annehmen. Wenn  , dann
, dann 
Weitere Details
In den folgenden Unterabschnitten finden Sie weitere Details zur Exponentialverteilung.
Memoryless-Eigenschaft
Eine der wichtigsten Eigenschaften der Exponentialverteilung ist die memoryless-Eigenschaft:  für jede
für jede  .
.
Dies wird wie folgt bewiesen: 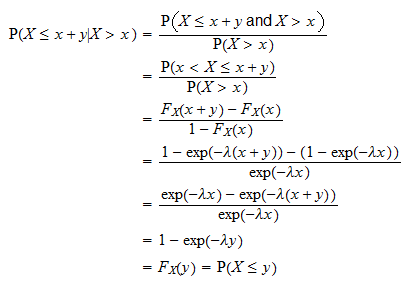
 ist die Zeit, die wir vor einem bestimmten Ereignis warten müssen tritt ein. Die obige Eigenschaft besagt, dass die Wahrscheinlichkeit, dass das Ereignis während eines Zeitintervalls der Länge
ist die Zeit, die wir vor einem bestimmten Ereignis warten müssen tritt ein. Die obige Eigenschaft besagt, dass die Wahrscheinlichkeit, dass das Ereignis während eines Zeitintervalls der Länge  auftritt, unabhängig davon ist, wie viel Zeit bereits vergangen ist (
auftritt, unabhängig davon ist, wie viel Zeit bereits vergangen ist ( ) ohne dass das Ereignis eintritt.
) ohne dass das Ereignis eintritt.
Die Summe der exponentiellen Zufallsvariablen ist eine Gamma-Zufallsvariable.
Angenommen,  ,
,  , …,
, …,  sind
sind  voneinander unabhängige Zufallsvariablen mit Exponentialverteilung mit dem Parameter
voneinander unabhängige Zufallsvariablen mit Exponentialverteilung mit dem Parameter  .
.
Definiere 
Dann ist die Summe  eine Gamma-Zufallsvariable mit den Parametern
eine Gamma-Zufallsvariable mit den Parametern  und
und  .
.
Dies wird anhand des Moments bewiesen Erzeugungsfunktionen (denken Sie daran, dass die Momenterzeugungsfunktion einer Summe voneinander unabhängiger Zufallsvariablen nur das Produkt ihrer Momenterzeugungsfunktionen ist):  Letzteres ist die Momenterzeugungsfunktion eines Gammas Verteilung mit den Parametern
Letzteres ist die Momenterzeugungsfunktion eines Gammas Verteilung mit den Parametern  und
und  .
.  hat also eine Gamma-Verteilung, da zwei Zufallsvariablen dieselbe Verteilung haben, wenn sie dieselbe Momenterzeugungsfunktion haben.
hat also eine Gamma-Verteilung, da zwei Zufallsvariablen dieselbe Verteilung haben, wenn sie dieselbe Momenterzeugungsfunktion haben.
Die Zufallsvariable  soll manchmal auch eine Erlang-Verteilung haben. Die Erlang-Verteilung ist nur ein Sonderfall der Gamma-Verteilung: Eine Gamma-Zufallsvariable ist auch eine Erlang-Zufallsvariable, wenn sie als Summe exponentieller Zufallsvariablen geschrieben werden kann.
soll manchmal auch eine Erlang-Verteilung haben. Die Erlang-Verteilung ist nur ein Sonderfall der Gamma-Verteilung: Eine Gamma-Zufallsvariable ist auch eine Erlang-Zufallsvariable, wenn sie als Summe exponentieller Zufallsvariablen geschrieben werden kann.
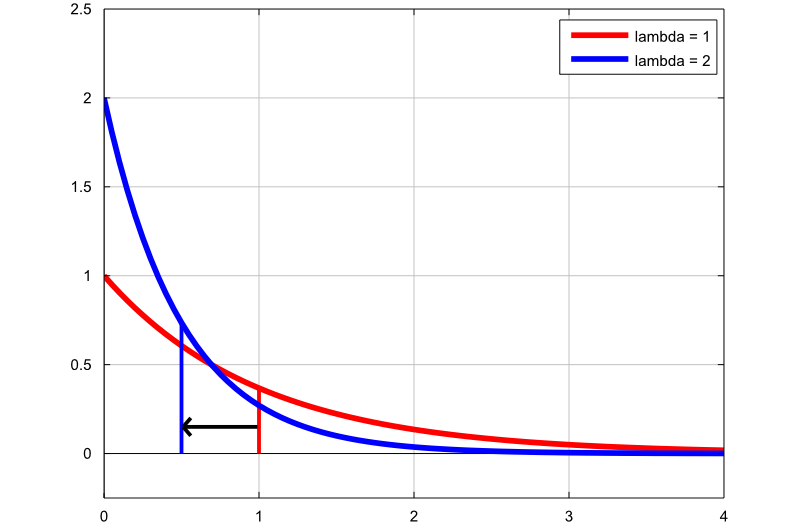
Dichtediagramm
Das nächste Diagramm zeigt, wie sich die Dichte der Exponentialverteilung durch Ändern des Ratenparameters ändert:
-
Der erste Graph (rote Linie) ist die Wahrscheinlichkeitsdichtefunktion einer exponentiellen Zufallsvariablen mit dem Ratenparameter
 ;
; -
Der zweite Graph (blaue Linie) ist die Wahrscheinlichkeitsdichtefunktion einer exponentiellen Zufallsvariablen mit dem Ratenparameter
 .
.
Die dünnen vertikalen Linien geben die Mittelwerte der beiden Verteilungen an. Beachten Sie, dass wir durch Erhöhen des Ratenparameters den Mittelwert der Verteilung von  auf
auf  verringern.
verringern.
Gelöste Übungen
Nachfolgend finden Sie einige Übungen mit erklärten Lösungen.
Übung 1
Sei  eine exponentielle Zufallsvariable mit dem Parameter
eine exponentielle Zufallsvariable mit dem Parameter  . Berechnen Sie die folgende Wahrscheinlichkeit:
. Berechnen Sie die folgende Wahrscheinlichkeit: 
Zunächst können wir die Wahrscheinlichkeit als unter Verwendung der Tatsache, dass die Wahrscheinlichkeit, dass eine kontinuierliche Zufallsvariable einen bestimmten Wert annimmt, gleich Null ist (siehe Kontinuierliche Zufallsvariablen und Ereignisse mit einer Wahrscheinlichkeit von Null). Nun kann die Wahrscheinlichkeit in Form der Verteilungsfunktion von  als
als 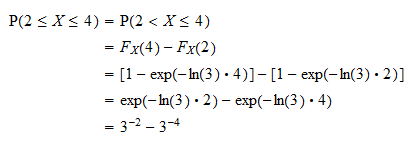
geschrieben werden Übung 2
Angenommen, die Zufallsvariable  hat eine Exponentialverteilung mit dem Parameter
hat eine Exponentialverteilung mit dem Parameter  . Berechnen Sie die folgende Wahrscheinlichkeit:
. Berechnen Sie die folgende Wahrscheinlichkeit: 
Diese Wahrscheinlichkeit kann mithilfe der Verteilungsfunktion von  :
: 
Aufgabe 3
Wie hoch ist die Wahrscheinlichkeit, dass eine Zufallsvariable  ist kleiner als der erwartete Wert, wenn
ist kleiner als der erwartete Wert, wenn  eine Exponentialverteilung mit dem Parameter
eine Exponentialverteilung mit dem Parameter  aufweist ?
aufweist ?
Der erwartete Wert einer exponentiellen Zufallsvariablen mit dem Parameter  ist
ist  Die obige Wahrscheinlichkeit kann mithilfe der Verteilungsfunktion von
Die obige Wahrscheinlichkeit kann mithilfe der Verteilungsfunktion von  berechnet werden:
berechnet werden: 
Zitieren
Bitte zitieren als: