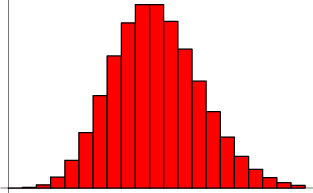
Poissonova distribuce
Vzhledem k Poissonovu procesu je pravděpodobnost získání přesně 
úspěchů v 
zkouškách dána limitem binomické distribuce
 |
(1)
|
Zobrazení distribuce jako funkce očekávaného počtu úspěchů
 |
(2)
|
místo velikosti vzorku 
pro pevné 
se rovnice (2) stává
 |
(3)
|
Necháme-li velikost vzorku 
zvětšit, distribuce se poté přiblíží
 |
 |
 |
(4)
|
 |
 |
 |
(5)
|
 |
 |
 |
(6)
|
 |
 |
 |
(7)
|
 |
 |
 |
(8)
|
známé jako Poissonovo rozdělení (Papoulis 1984, s. 101 a 554; Pfeiffer a Schum 1973, str. 200). Všimněte si, že velikost vzorku 
zcela vypadla z funkce pravděpodobnosti, která má stejný funkční tvar pro všechny hodnoty 
.
Poissonovo rozdělení je implementováno ve WolframLanguage jako Poissonovo rozdělení.
Podle očekávání je Poissonovo rozdělení normalizováno tak, že součet pravděpodobností je roven 1, protože
 |
(9 )
|
Poměr pravděpodobností je dán
 |
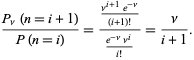(10)
|
Poissonovo rozdělení dosáhne maxima, když
 |
(11)
|
kde je Euler-Mascheroniho konstanta a 
harmonické číslo, které vede k transcendentální rovnici
 |
(12)
|
které nelze vyřešit přesně pro 
.
Funkce generování momentů distribuce Poisson je dána
 |
 |
 |
(13)
|
 |
 |
 |
(14)
|
 |
 |
 |
(15)
|
 |
 |
 |
(16)
|
 |
 |
 |
(17)
|
 |
 |
 |
(18)
|
tak
 |
 |
 |
(19)
|
 |
 |
 |
(20)
|
(Papoulis 1984, str. 554).
Nezpracované momenty lze také vypočítat přímo součtem, čímž se získá neočekávané spojení s Bellovým polynomiálním 
a Stirlingovým číslem druhého druhu,
 |
(21)
|
známý jako Dobińského vzorec.Proto
 |
 |
 |
(22)
|
 |
 |
 |
(23)
|
 |
 |
 |
(24)
|
Ústřední momenty lze poté vypočítat jako
 |
 |
(25)
|
|
 |
 |
 |
(26)
|
 |
 |
 |
(27)
|
takže průměr, rozptyl, šikmost a převýšení jsou
 |
 |
 |
(28)
|
| |
 |
 |
(29)
|
 |
 |
 |
(30)
|
 |
 |
 |
(31)
|
 |
 |
 |
(32)
|
Charakteristická funkce pro Poissondistribuci je
(Papoulis 1984, s. 154 a 554) a funkce generující kumulant je
 |
(34)
|
tak
 |
(35)
|
Střední odchylka Poissonova rozdělení je dána
 |
(36)
|
Poissonovo rozdělení lze vyjádřit také pomocí
 |
(37)
|
 |
(38)
|
Funkce generování momentů distribuce aPoisson ve dvou proměnných je dána
 |
(39)
|
Pokud jsou nezávislé proměnné 
, 
, …, 
mít Poissonovy distribuce s parametry 
, 
, …, 
, pak
 |
(40)
|
má Poissonovo rozdělení s parametrem
 |
(41)
|
Je to vidět, protože funkce generující kumulant je
 |
(42)
|
 |
(43)
|
Zobecnění Poissonovy distribuce použil Saslaw (1989) k modelování pozorované shlukování galaxií ve vesmíru. Forma této distribuce je dána
 |
(44)
|
kde 
je počet galaxií v objemu 
, 
, 
je průměrná hustota galaxií a 
, přičemž 
je poměr gravitační energie k kinetické energie zvláštních pohybů, Letting 
dává
 |
(45)
|
což je skutečně Poissonova distribuce s 
. Podobně necháme 
dát 
.