Měření: Objevování vzorců pro oblast

Vzorce oblasti

Studenti, kteří mají neformální představu, že oblast je „částkou 2D“ „věci“ ”obsažené v regionu si mohou sami vymyslet většinu vzorců, které jsou často požadovány pouze k zapamatování. Každý vzorec, který znovu objevují, pomáhá posílit jejich porozumění (a paměť) pro ostatní vzorce, které znají. (Viz také povrchová plocha.)

Plocha obdélníků

Výběrem čtverce jako jednotky plochy získáme intuitivní představu o ploše obdélníků. Pokud se rozhodneme, že plocha tohoto čtverce je 1, pak obdélník , který je 7krát delší, bude mít 7 × 1 jako jeho oblast.

Obdélník, který je dvakrát větší než , by měl dvojnásobnou plochu, takže oblast je 2 × 7 jednotek plochy. Můžeme spočítat dvě řady sedmi čtverců. Podobně má 3 řady po 7 čtvercích (nebo 7 sloupců po 3 čtvercích), celkem tedy 7 × 3 čtverce, takže její plocha je 21 čtverečních jednotek.

Počet čtverců v jednom řádku je délka obdélníku. Počet řádků je výška obdélníku. Takže plocha je délka × výška.

Protože obdélník lze nakreslit šikmo, „výška“ je definována jako „směr kolmý k základně“ a „základna“ je definována jako, ať už si vyberete jakoukoli stranu.

To funguje pro počítání čísel. Funguje to dokonce i pro zlomky. 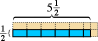Zde zobrazený modrý obdélník měří polovinu délková jednotka vysoká o pět a půl délkové jednotky široká. Pokud jako oblastní jednotku zvolíme odpovídající čtverec, zjistíme, že modrý obdélník obsahuje pět polovičních jednotek plochy a jednu čtvrtinovou jednotku plochy, nebo celkem dvě a tři čtvrtiny jednotky plochy. (Růžové části ukazují dokončení každé čtvercové jednotky plochy.)

Abychom zahrnuli všechna čísla, definujeme plochu obdélníku jako základnu × výšku (kde „základna“ a „výška“ znamenají délky těchto stran, měřeno ve stejných jednotkách).

Plocha rovnoběžníků

Získání nápadu

Můžeme zjistit vzorec pro plochu rovnoběžníku pomocí pitvy rovnoběžník a přeskupení dílů tak, aby vznikl obdélník. Protože rovnoběžník a obdélník jsou složeny ze stejných částí, musí mít nutně stejnou plochu. (Další informace o tom, proč jsou tyto oblasti stejné, najdete v definici oblasti.)

Vidíme, že také mají přesně stejnou délku základny (modrá) a přesně stejnou výšku (zelená). Protože základna × výška udává plochu obdélníku, můžeme k výpočtu její plochy použít stejná měření na rovnoběžníku: základna × výška. (Stejně jako dříve se „výška“ měří kolmo na základnu a „základna“ je na kterékoli straně, kterou jste vybrali jako první. Viz rovnoběžník.)

Výřez zobrazený výše usnadňuje zjištění, že délka základny je beze změny. Ve skutečnosti lze kolmý řez provést kdekoli podél základny.

Vyřezávání otvorů

Intuice a důkaz

Tato pitva poskytuje intuitivní pochopení vzorce plochy pro rovnoběžník, což je důvod, proč by měl být takový, jaký je. Ale nezpochybňovali jsme, zda pitva skutečně „funguje“. To znamená, že když vyřízneme rovnoběžník a uspořádáme jeho části, očekáváme, že dostaneme a výsledek určitě vypadá. Ale zdání může být klamné. Co nás ujišťuje, že když posuneme tento trojúhelník, výsledkem bude obdélník? Co když je to spíš (i když méně přehnané)? Pokud výsledek není vždy dokonalý obdélník, nemůžeme použít naše znalosti vzorce plochy obdélníku k vytvoření vzorce pro rovnoběžník. Na střední škole budou studenti schopni dokázat, že pokud jsou obě části rovnoběžníku správně sestaveny, vytvoří obdélník . V ročnících K-8 se studenti většinou musí spolehnout na vizuální experiment a musí mít intuitivní pocit. Další informace o tom, proč tyto pitvy fungují.

Co když jako základ vybereme krátkou stranu?

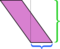
Jako základnu si můžeme zvolit libovolnou stranu; „výška“ je definován jako měřeno kolmo na stranu, kterou zvolíme jako základnu. Vezmeme-li jako základ krátkou stranu (modrou), není výše uvedená pitva tak přesvědčivá. Proříznutí této výšky a nové uspořádání částí zanechává nepořádek:

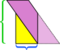
V tomto konkrétním příkladu nepořádek můžeme zachránit tím, že uděláme ještě jeden řez, 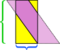, ale co kdyby byl rovnoběžník ještě delší a štíhlejší?

Ukazuje se, že jakýkoli rovnoběžník, bez ohledu na to, jak dlouhý a hubený, může být takto rozřezán, takže části – snad mnoho z nich – lze přeskupit do obdélníku. Chce to však více práce, než se ukáže, že toho lze vždy dosáhnout. Potřebujeme další nápad.

Trochu odlišná myšlenka pitvy v tomto případě usnadňuje život. (Sami můžete ukázat, že to funguje i v původním případě.)

• Uzavřete rovnoběžník do obdélníku.
• Dvě části obdélníku, které nejsou uvnitř rovnoběžníku, jsou shodné trojúhelníky.
• Posuňte jeden z těchto trojúhelníků směrem k druhému, dokud se nesetkají, aby vytvořily obdélník. 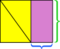Protože se celková plocha vnějšího obdélníku nezměnila (jedná se o stejný obdélník jako dříve) a žlutá oblast se nezměnila (jednotlivé části se právě pohybovaly), rozdíl mezi ty – fialové oblasti – musí být stejné. Stejně jako dříve můžeme také vidět, že rozměry obdélníkové fialové oblasti jsou základnou a výškou původního rovnoběžníku.

Intuice a důkaz, repríza : Znovu pitva poskytuje základní vhled, ale zabere to trochu více práce, aby bylo zajištěno, že dva žluté trojúhelníky, které rozhodně vypadají, jako by do sebe zapadaly, aby vytvořily obdélník, skutečně zapadají přesně, a ne téměř.

Proč je důležité být tak opatrní?

Když budeme vytvářet další vzorce oblastí (níže), budeme chtít použít náš způsob, jak najít oblast rovnoběžníku, a tak chceme abychom se mohli spolehnout na pravidlo, které jsme našli. Můžeme si být jisti, že přeskupení dílů nezmění oblast: to je koneckonců to, jak definujeme oblast. Musíme si však také být jisti, že díly do sebe zapadají tak, jak tvrdíme, že jsou, nebo se nemůžeme spolehnout na měření, která jsme provedli. A musíme si být jisti, že pravidlo základu × výšky nezávisí na šťastném výběru základny.

Ve většině učebních plánů nemají studenti před 8. ročníkem dostatečně systematickou základnu geometrických znalostí, aby mohli zvukové důkazy, že tyto pitvy fungují. Ale intuitivní porozumění stačí k vysvětlení a ospravedlnění vzorců a je dobrým základem pro pozdější geometrické studium.

Plocha trojúhelníku

Znalost, jak najít plochu rovnoběžníku, nám pomáhá najděte oblast trojúhelníku.

Členění trojúhelníku

Trojúhelník můžeme rozdělit na dvě části – jednu z nich na trojúhelník a jednu na lichoběžník – tak, že jej rozkrojíte rovnoběžně na základnu. Pokud s tímto řezem vyřízneme výšku přesně na polovinu, obě části do sebe zapadnou a vytvoří rovnoběžník se stejnou základnou, ale s poloviční výškou.

Takže základna × poloviční výška udává plochu trojúhelníku. Podobná pitva ukazuje poloviční základnu × výšku. Kterýkoli z nich se zmenší na bh.

Zdvojnásobení trojúhelníku a následná polovina výsledné oblasti

Další způsob myšlení: dvě kopie trojúhelník vytvoří rovnoběžník se stejnou základnou a stejnou výškou jako trojúhelník.

Plocha rovnoběžníku je základna × výška, ale to je dvojnásobná plocha trojúhelníku, takže plocha trojúhelníku je základny × výšky, jak jsme viděli u metody pitvy.

(Jako vždy , vyberte „základnu“ a změřte výšku kolmou k této základně, od základny k opačnému vrcholu.)

Oblast lichoběžníku

Zdvojnásobení lichoběžníku a následná polovina výsledné oblasti

Jak to u trojúhelníku platilo, dvě kopie lichoběžníku lze spojit dohromady a vytvořit rovnoběžník.

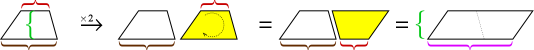
Výška rovnoběžníku je stejná jako výška lichoběžníku, ale jeho základna je součtem dvou základen lichoběžníku. Plocha rovnoběžníku je tedy výška × (základna1 + základna2). Ale tato oblast jsou dva lichoběžníky, takže ji musíme snížit na polovinu, abychom získali plochu lichoběžníku.

Pitva lichoběžníku

Mohli bychom také lichoběžník pitvat způsobem, který jsme pitvali trojúhelník s jediným řezem, který snižuje jeho výšku na polovinu. Obě části do sebe zapadají a vytvářejí rovnoběžník, jehož základna je součtem dvou základen lichoběžníku, ale jejíž výška je poloviční než výška lichoběžníku.

V případě lichoběžníku nemohou základny být vybrán dle libosti. Dvě rovnoběžné strany jsou základny a výška, jako vždy, je kolmá vzdálenost od jedné základny k opačné.

Plocha tohoto rovnoběžníku je jeho výška (poloviční výška lichoběžníku) krát jeho základna (součet základen lichoběžníku), takže jeho plocha je poloviční výšky × (základna1 + základna2). Protože rovnoběžník je vyroben z přesně stejného „materiálu“ jako lichoběžník, je to také oblast lichoběžníku.

Ať tak či onak, plocha lichoběžníku je × výška × (základna1 + základna2).

Plocha dalších speciálních čtyřúhelníků

Plocha kosočtverce

Plochu kosočtverce lze najít rozřezáním a přeskupením dílků za účelem vytvoření rovnoběžníku. To lze provést několika způsoby:

1. Prořízněte kratší úhlopříčku (a) a vytvořte dva shodné trojúhelníky. Přesuňte dolní polovinu trojúhelníku vedle horní poloviny a vytvořte rovnoběžník. Kratší úhlopříčka (a) se stane základnou rovnoběžníku a polovina delší úhlopříčky (b) se stane výškou rovnoběžníku. Plocha kosočtverce je tedy * b nebo součin úhlopříček, což je standardní vzorec pro kosočtverec.
2. Dalším podobným způsobem je rozřezat kosočtverec na čtyři shodné trojúhelníky a přeskupit je do obdélníku s kratší úhlopříčkou jako základnou a polovinou delší úhlopříčky jako výška.
3. Po řezání kosočtverec do dvou shodných trojúhelníků, můžeme vypočítat plochu jednoho z trojúhelníků, což je * base (a) * height ( b) = ab. Pak vynásobte dvěma, protože jsou dva: 2 * ab = ab.

Plocha draka

Plochu draka lze najít podobně jako oblast kosočtverce. Řezání přes delší úhlopříčku poskytuje dva shodné trojúhelníky. Pokud je uspořádáme, můžeme vytvořit rovnoběžník s delší úhlopříčkou (b) jako základnou a polovinou kratší úhlopříčky (a) jako výšky. Oblast se tedy stane b * a = ab. Složitější přístup zahrnuje trochu algebry. Vystřihněte draka přes kratší úhlopříčku a vytvořte dva trojúhelníky s kratší úhlopříčkou (a) jako základnou. Plocha prvního trojúhelníku je tedy a * squiggly, kde squiggly je výška. Plocha druhého trojúhelníku je a * (b – squiggly), kde (b – squiggly) je zbývající část delší úhlopříčky. Celková plocha se tak stane ( a * squiggly) + ( a * (b – squiggly)). Z faktoringu a máme a (squiggly + b – squiggly) = ab.

No, co víš. V zásadě potřebujete znát pouze vzorec pro oblast rovnoběžníku a poté odvodit vzorec pro ostatní.