Jak vypočítat plochu

Výpočet plochy

Plocha se měří ve čtvercích (nebo v čtvercových jednotkách).

Kolik čtverců je v tomto obdélníku?

Můžeme spočítat čtverce nebo můžeme vezměte délku a šířku a použijte násobení. Výše uvedený obdélník má plochu 15 čtverečních jednotek.

Plocha obdélníku je = délka x šířka

Příklady výpočtu plochy obdélníku

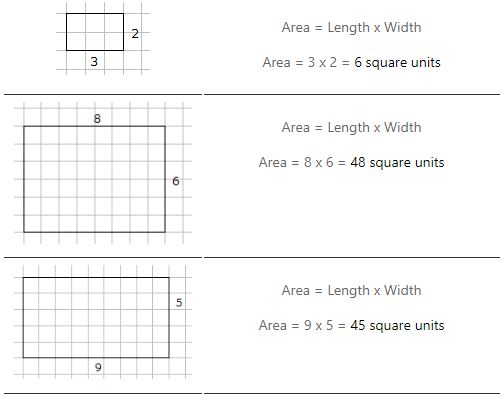
Jednotky pro měření plochy

Měříme plochu pomocí čtverců. Používáme různé velikosti čtverců podle toho, jak velká nebo malá je plocha.

Příklad	délka strany na čtvercích	jednotka
velikost hřebík na palec	milimetr	mm2
velikost papíru	centimetr	cm2
Velikost místnosti	Měřič	m2
Velikost města	Kilometr	km2

Nezapomeňte na malou 2

Čtvercové velikosti píšeme pomocí malé 2 vedle jednotky.
Píšeme mm2, cm2, m2, km2, cm2
Můžeme říci „63 milimetrů na druhou“ nebo „63 milimetrů čtverečních“

K měření velkých ploch bychom mohli použít malé čtverce. Jediným problémem je, že bychom nakonec museli použít velmi velké čísla. Například pole může být měřeno na 5 000 000 000 milimetrů čtverečních, když 5 000 metrů čtverečních by bylo mnohem snazší říci, psát a vizualizovat.

Pravděpodobně uslyšíte více jednotek pro měření plochy; čtvereční palce, čtvereční stopy, čtvereční yardy, čtvereční míle, akr, hektar jsou všechny jednotky používané k měření plochy.

Další příklady výpočtu plochy

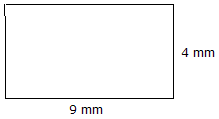	Plocha = délka x šířka Plocha = 9 mm x 4 mm = 36 mm2
	Plocha = Délka x Šířka Plocha = 7 cm x 6 cm = 42 cm2
	Plocha = Délka x Šířka Plocha = 8 mx 2 m = 16 m2
	Plocha = Délka x Šířka Plocha = 7 km x 5 km = 35 km2

Plocha čtverce

Délka a šířka čtverce jsou stejné, takže stačí vynásobit délku délkou.

Plocha = Délka x Délka Plocha = 6 cm x 6 cm = 36 cm2

Plocha kruhu

Plocha kruhu = πr2
kde r je poloměr kruhu a π je poměr obvodu kruhu k jeho průměru.

π (vyslovuje se „koláč“ a často se píše „Pi“) je nekonečné desetinné místo se společnou přibližná hodnota 3,14159. Více informací o Pi najdete zde

Příklad výpočtu plochy kruhu

Area = πr2 Area = 3,14159 x (4 cm) 2 Plocha = 3,14159 x 16 cm2 Plocha = 50,27 cm2 Odpověď zaokrouhleno na 2 desetinná místa

Vysvětlení oblasti vzorce kruhu

Vezměte kruh a rozdělte jej na stejně velké sektory a uspořádat je, jak je znázorněno níže. Všimněte si, jak se sektory zmenšují a tvar se podobá spíše obdélníku. Poznámka: Neexistuje žádné omezení toho, jak malé mohou být tyto sektory a do jaké míry by se mohly podobat obdélníku, když jsou uspořádány.

Za předpokladu, že víme, že obvod kruhu je roven 2πr, můžeme přidat rozměry „obdélník“, jak je znázorněno níže. Pomocí plochy vzorce plochy obdélníku, area = width x height vidíme, jak může být ukázáno, že náš kruh, překonfigurovaný jako obdélník, má plochu, která se blíží πr xr nebo πr2

Kruh Přeskupené sektory

Přeskupené sektory kruhů – začíná vypadat jako obdélník

oblast Složené tvary

Existuje mnoho případů, kdy výpočet celkové plochy vyžaduje výpočet více než jedné oblasti, po které následuje přidání, odčítání nebo jiná kombinace operací k nalezení požadované oblasti.

Poznámka: V níže uvedených příkladech nejsou jednotky měření zobrazeny a odpovědi a hodnota π (Pi) byly zaokrouhleny na nejbližší setinu.

Příklad: Jednoduché složené tvary

Níže uvedený příklad výpočtu plochy je poměrně jednoduchý. Tvar lze chápat jako trojúhelník kombinovaný s obdélníkem.

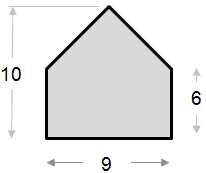Plocha trojúhelníkové části: ½ x základna x výška ½ x 9 x 4 = 18 Plocha obdélníkové části: šířka x výška 9 x 6 = 54 Celková plocha = 18 + 54 = 72

Výše uvedený příklad ilustruje běžný požadavek při práci se sloučeninou tvary – nalezení kót, které nejsou zobrazeny. Při doučování svých dětí poskytněte v případě potřeby pomoc s nalezením těchto „chybějících“ dimenzí. Níže je uveden další příklad.

Hledání dimenzí

Jaké jsou rozměry malé obdélníkové části? Šířka? 12 – 7 – 2 = 3 Výška? 8 – 6 = 2

Příklad: Odečtení jedné oblasti od druhé

V níže uvedeném příkladu lze tvar vidět jako obdélník s vyříznutým trojúhelníkem.

Plocha obdélníkové části: šířka x výška 5 x 6 = 30 Plocha trojúhelníkové části: ½ x základna x výška ½ x 3 x 3 = 4,50 Celková plocha = 30 – 4,50 = 25,50

Příklad: Částečné oblasti

Níže uvedený příklad je podobný příkladu výše, protože protože máme půlkruh, musíme vypočítat zlomek (polovinu) oblasti kruhu. V tomto příkladu je uveden průměr, nikoli poloměr.

Plocha trojúhelníkové části: ½ x základna x výška ½ x 6 x 6 = 18 Plocha půlkruhové části: ½ x (πr2) ½ x (3,14 x 1,52) = 3,53 Celková plocha = 18 – 3,53 = 14,47

Příklad: Rozhodnutí! Kombajn? Odečíst

Je běžné, že existuje více než jeden způsob výpočtu konečné plochy. V níže uvedených příkladech lze tvar vidět jako dva obdélníky kombinované nebo jako jeden velký obdélník s menším obdélníkem „vystřiženým“ z pravého horního rohu.

Pracovní listy pro výpočet oblasti

Tisk rozvrhněte níže uvedené listy a použijte je pro nácvik výuky svých dětí.

• Výpočet ploch – obdélníky a čtverce
• Výpočet ploch – obdélníky
• Výpočet Oblasti – Obdélníky
• Výpočet složených oblastí, např s obdélníkovými tvary
• Výpočet složených ploch např. s obdélníky, trojúhelníky a kruhy
• Výpočet oblastí, např. trojúhelníků
• Plocha kruhu
• Výpočet povrchových ploch např. pravoúhlých hranolů

Zde najdete další tisknutelné listy geometrie.