Jak vypočítat objem

Výpočet objemu

Objem se měří v kostkách (nebo v kubických jednotkách).

Kolik kostek je v tomto obdélníkovém hranolu (kvádr)?

Můžeme spočítat kostky, i když je rychlejší vzít délku, šířku a výšku a použít násobení. Výše uvedený obdélníkový hranol má objem 48 kubických jednotek.

Objem pravoúhlého hranolu je = délka x šířka x výška

Příklady výpočtu plochy obdélníku

Abychom svazek vyřešili, musíme udělat dvě násobení. Vypočítáme plochu jedné plochy (nebo strany) a vynásobíme ji její výškou. Níže uvedené příklady ukazují, jak existují tři způsoby.

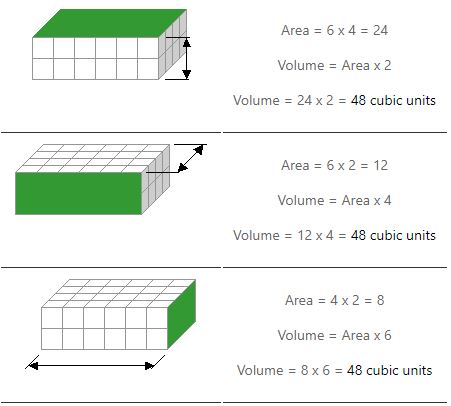
Všimněte si, jak dostáváme stejnou odpověď bez ohledu na to, jakou stranu použijeme k nalezení oblasti.

Když vaše dítě začne pracovat s oblastí a obvodem, bude obvykle pracovat se 2 dimenzemi – čtverce, obdélníky, trojúhelníky atd., které jsou na papíře zobrazeny jako ploché – neexistuje žádná hloubka ani třetí rozměr. Práce s objemem zahrnuje 3 dimenze. Zajistěte, aby si to vaše dítě uvědomovalo a nemyslelo si na kostky a další 3D tvary zobrazené na papíře jako jen na další „tvar na stránce“. Ukažte jim skutečná pole a ukažte, jak je lze nakreslit (nebo znázornit) na dvourozměrný kus papíru. Jinými slovy, ujistěte se, že existuje spojení mezi tím, co je na papíře, a tím, co představuje ve skutečném světě.

Ujistěte se, že vaše dítě není zmateno použitím hlasitosti, jaká se používá při mluvení o hlasitosti .

Jednotky pro měření objemu

Mezi jednotkami měření objemu jsou velmi velké rozdíly. Například v 1 metru je 100 centimetrů, ale je jich 1 000 000 (ano, 1 milion ) centimetry krychlové v metru krychlovém.

Proč velký rozdíl? Protože v objemu nemáme jen délku; máme délku, šířku a výšku. Níže to ukazuje příklad kostky cukru.

Kolik cukru? 1 m3 nebo 1 000 000 cm3

Přemýšlejte o naplnění velmi velké krabice (která by byla 1 metr široká, 1 metr, dlouhá a jeden metr vysoká) kostkami cukru (každou strana 1 centimetr).

	Krok 1: jeden řádek ve spodní části pole – to by bylo 100 kostky cukru
	Krok 2: zakryjte zbytek základny krabice – , což by dalo celkem 100 řádků s 100 kostek cukru. 100 x 100 = 10 000 cukru kostky ve spodní části velké krabice.
	Krok 3: Opakujte to 99krát, dokud nebude vrstvy 10 000 kostek naskládaných do 100 hlubokých vrstev. 10 000 x 100 = 1 000 000 kostek cukru

V 1 m3 je 1 000 000 cm3 – dávejte pozor, abyste neměli příliš mnoho cukru!

Existují i jiné jednotky pro měření objemu; kubické palce, kubické stopy, kubické yardy jsou všechny jednotky používané k měření objemu. Mililitry, litry, galony se také používají zejména při měření kapalin.

Nezapomeňte na druhou 3

Píšeme kubické velikosti pomocí malé 3 vedle jednotky.
Píšeme mm3, cm3, m3, km3, cm3
Můžeme říci „85 centimetrů krychlových“ nebo „85 centimetrů krychlových“

Příklady výpočtu objemu obdélníkových hranolů

	Hlasitost = délka x šířka x výška Objem = 12 cm x 8 cm x 6 cm = 576 cm3
	Objem = délka x šířka x výška objem = 20 mx 2 mx 2 m = 80 m3
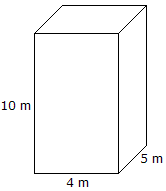	Objem = Délka x Šířka x Výška objem = 10 mx 4 mx 5 m = 200 m3

Objem válce

Výpočet objemu válce der zahrnuje vynásobení plochy základny výškou válce. Základna válce je kruhová a vzorec pro plochu kruhu je: plocha kruhu = πr2. V oblasti kruhu je toho víc.

Objem = Plocha základny x Výška Objem = πr2 xh Objem = πr2 h

Poznámka: v níže uvedených příkladech použijeme 3.14 jako přibližnou hodnotu pro π (Pi).

Příklad výpočtu objemu válce

Rozměry jsou v cm.

Hlasitost = πr2 h Hlasitost = 3.14 x 3 x 3 x 8 Objem = 226,08 cm3

Objem kužele

Objem kužele se rovná jedné třetině objemu válce se shodnou výškou a plochou základny. Získáte vzorec pro objem kužele, jak je uvedeno níže.

Volume = 1/3 πr2h

Příklad výpočtu objemu kužele

Rozměry jsou v cm.

Objem = 1/3 πr2 h Objem = 1/3 x 3,14 x 2 x 2 x 7 Objem = 29,31 cm3

Objem koule

Vzorec pro objem koule je uveden níže.

Volume = 4/3 πr3

Příklad výpočtu objemu koule

Rozměry jsou v cm.

Hlasitost = 4/3 πr3 Hlasitost = 4/3 x 3,14 x 4 x 4 x 4 Objem = 267,95 cm3

Tiskové listy svazků k tisku

Následující tabulka slouží k procvičení výpočtu svazků.

• Hledání svazku v kubických jednotkách – obdélníkové hranoly a kompozity
• Objemy obdélníkových hranolů
• Objemy obdélníkových hranolů
• Objemy objektů „reálného světa“, např. krabic s obilninami
• Výpočet objemů např. trojúhelníkových hranolů a válců

Další listy geometrie získáte po obvodu, ploše a dalších zde.