Exponenciální distribuce
Marco Taboga, PhD
Exponenciální distribuce je spojité rozdělení pravděpodobnosti používané k vymodelujte čas, který musíme počkat, než dojde k dané události. Je to spojitý protějšek geometrického rozdělení, které je místo toho diskrétní.
Někdy se mu říká také záporné exponenciální rozdělení.
Úvod
Kolik času uplyne, než v dané oblasti dojde k zemětřesení? Jak dlouho musíme čekat, než zákazník vstoupí do našeho obchodu? Jak dlouho bude trvat, než call centrum přijme další telefonní hovor? Jak dlouho bude stroj fungovat bez poškození?
Na otázky, jako jsou tyto, se často odpovídá pravděpodobnostním způsobem pomocí exponenciálního rozdělení.
Všechny tyto otázky se týkají času, který potřebujeme čekat, než dojde k dané události. Pokud tato čekací doba není známa, je často vhodné ji považovat za náhodnou proměnnou s exponenciálním rozdělením.
Zhruba řečeno, čas 
potřebujeme čekat, než dojde k události, má exponenciální rozdělení, pokud je pravděpodobnost, že k události dojde během určitého časového intervalu, úměrná délce daného časového intervalu.
Přesněji řečeno, má exponenciální rozdělení, pokud je podmíněná pravděpodobnost přibližně úměrná délce časového intervalu mezi časy a kdykoli .
V mnoha praktických situacích je tato vlastnost velmi realistická. To je důvod, proč je exponenciální distribuce tak široce používána k modelování čekacích dob.
Exponenciální distribuce úzce souvisí s Poissonovým rozdělením. Pokud 1) událost může nastat vícekrát a 2) čas uplynulý mezi dvěma po sobě jdoucími výskyty je exponenciálně distribuován a nezávislý na předchozích výskytech, pak má počet výskytů události v dané jednotce času Poissonovo rozdělení. Vyzýváme čtenáře, aby si přečetl přednášku o Poissonově rozdělení pro podrobnější vysvětlení a intuitivní grafické znázornění této skutečnosti.
Definice
Exponenciální rozdělení je charakterizováno následovně.
Definice Nechť být spojitá náhodná proměnná. Nechť je jeho podporou množina kladných reálných čísel: Nechť . Říkáme, že má exponenciální rozdělení s parametrem právě tehdy, pokud je jeho funkce hustoty pravděpodobnosti Parametr se nazývá parametr rychlosti.
Náhodná proměnná s exponenciálním rozdělením se také nazývá exponenciální náhodná proměnná.
Následuje důkaz, že je legitimní funkce hustoty pravděpodobnosti.
Nezápornost je zřejmá. Musíme dokázat, že integrál přes se rovná . To dokazujeme následovně:
Abyste lépe porozuměli exponenciálnímu rozdělení, můžete se podívat na jeho grafy hustoty.
Parametr rychlosti a jeho interpretace
Zmínili jsme, že pravděpodobnost, že k události dojde mezi dvěma daty a je úměrný (podmíněno informacemi, že k němu nedošlo před ). Parametr sazby je konstanta proporcionality: kde je nekonečná hodnota vyšší řád než (tj. funkce , která se vynuluje rychleji než does).
Výše uvedená podmínka proporcionality postačuje také k úplné charakteristice exponenciálního rozdělení.
Návrh Podmínka proporcionality je spokojen, pouze pokud má exponenciální rozdělení.
Podmíněnou pravděpodobnost lze zapsat jako 
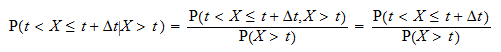Označte distribuční funkci , tj. a podle jeho funkce přežití: Potom rozdělením obou stran o , získáme kde je množství, které má sklon když má sklon . Vezmeme-li limity na obou stranách, získáme nebo podle definice derivátu: Tuto diferenciální rovnici lze snadno vyřešit pomocí řetězce pravidlo: Pokud vezmeme integrál z na obou stran, dostaneme a nebo Ale (protože nemůže nabývat záporné hodnoty) implikuje Exponentaci obou stran získáme Proto nebo Funkce hustoty je však první derivací distribuční funkce: a termín zcela vpravo je hustota exponenciální náhodné proměnné. Podmínka proporcionality je proto splněna, pouze pokud je exponenciální náhodná proměnná
Očekávaná hodnota
Očekávaná hodnota exponenciální náhodné proměnné je
Lze jej odvodit následovně: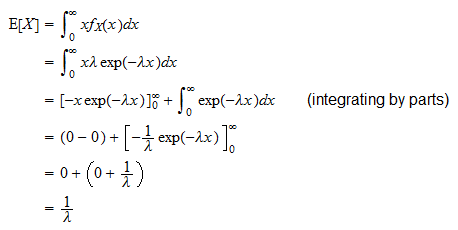 
Variance
Variance of exponenciální náhodná proměnná je
lze odvodit díky obvyklému variačnímu vzorci (): 
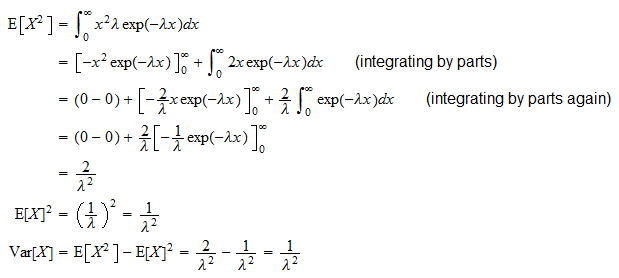
Funkce generování momentů
Funkce generování momentů exponenciální náhodné proměnné je definována pro jakoukoli :
Definice funkce generující moment dává Of výše uvedené integrály se samozřejmě sbíhají pouze v případě , tj. pouze v případě, že . Proto funkce generování momentů exponenciální náhodné proměnné existuje pro všechny .
Charakteristická funkce
Charakteristická funkce exponenciální náhodné proměnné je
Použitím definice charakteristické funkce a skutečnosti, že můžeme psát Nyní vypočítáme samostatně dva integrály . První integrál je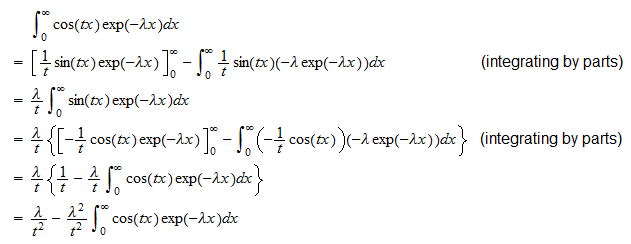 
Proto , který lze přeskupit, aby poskytl nebo Druhým integrálem je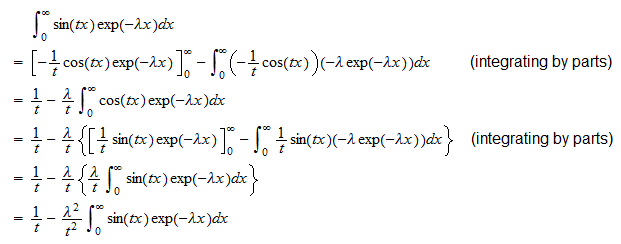 
Proto , které lze přeskupit a získat nebo Spojením dílků získáme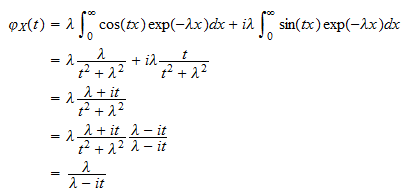 
Distribuční funkce
Distribuční funkce exponenciální náhodné proměnné je
Pokud , pak protože nemůže nabývat záporných hodnot. Pokud , pak
Další podrobnosti
V následujících podsekcích najdete další podrobnosti o exponenciálním rozdělení.
Vlastnost bez paměti
Jednou z nejdůležitějších vlastností exponenciálního rozdělení je vlastnost bez paměti: pro všechny .
Dokazuje se to takto: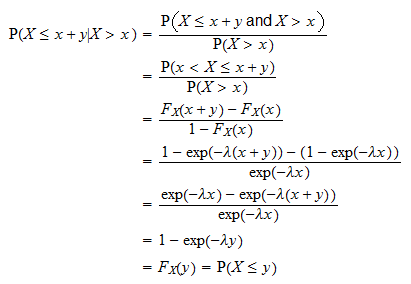 
je čas, který musíme počkat před určitou událostí dojde. Výše uvedená vlastnost říká, že pravděpodobnost, že k události dojde během časového intervalu délky , je nezávislá na tom, kolik času již uplynulo () bez toho, aby k události došlo.
Součet exponenciálních náhodných proměnných je náhodná proměnná gama
Předpokládejme , , …, jsou vzájemně nezávislé náhodné proměnné s exponenciálním rozdělením s parametrem .
Definujte
Součet je pak náhodná proměnná gama s parametry a .
To se dokazuje pomocí momentu funkce generování (pamatujte, že funkce generování momentů součtu vzájemně nezávislých náhodných proměnných je pouze produktem jejich funkcí generujících momenty): Ta druhá je funkcí generování momentů gama distribuce s parametry a . Takže má distribuci gama, protože dvě náhodné proměnné mají stejnou distribuci, když mají stejnou funkci generování momentů.
O náhodné proměnné se také někdy říká, že má Erlangovu distribuci. Distribuce Erlang je jen zvláštním případem distribuce gama: náhodná proměnná gama je také náhodnou proměnnou Erlang, když ji lze zapsat jako součet exponenciálních náhodných proměnných.
Graf hustoty
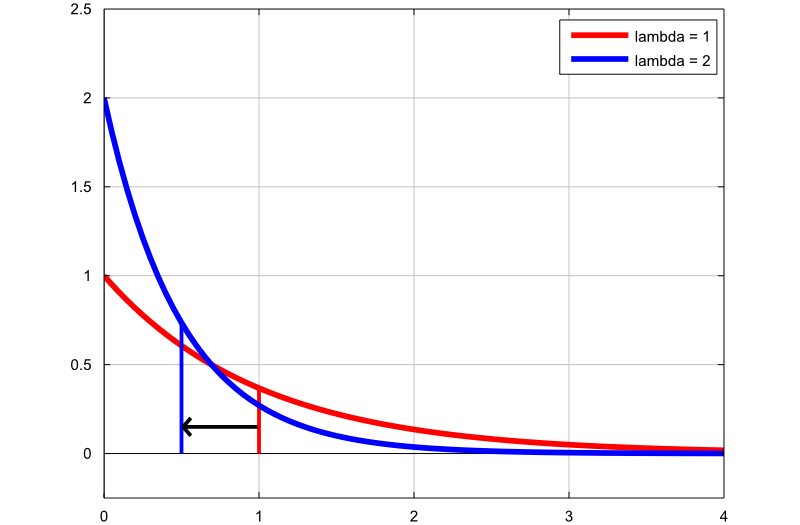
Následující graf ukazuje, jak se mění hustota exponenciálního rozdělení změnou parametru rychlosti:
-
první graf (červená čára) je funkcí hustoty pravděpodobnosti exponenciální náhodné proměnné s parametrem sazby
; -
druhý graf (modrá čára) je funkcí hustoty pravděpodobnosti exponenciální náhodné proměnné s parametrem sazby
.
Tenké svislé čáry označují průměr těchto dvou distribucí. Upozorňujeme, že zvýšením parametru rychlosti snížíme průměr distribuce z na .
Vyřešená cvičení
Níže naleznete některá cvičení s vysvětlenými řešeními.
Cvičení 1
Nechť být exponenciální náhodná proměnná s parametrem . Vypočítejte následující pravděpodobnost:
Nejprve můžeme pravděpodobnost napsat jako využití skutečnosti, že pravděpodobnost, že spojitá náhodná proměnná získá jakoukoli konkrétní hodnotu, se rovná nule (viz Kontinuální náhodné proměnné a události s nulovou pravděpodobností). Nyní lze pravděpodobnost zapsat z hlediska distribuční funkce jako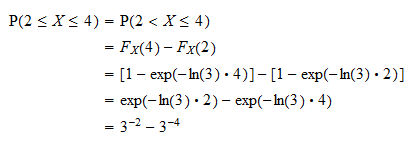 
Cvičení 2
Předpokládejme, že náhodná proměnná má exponenciální rozdělení s parametrem . Vypočítejte následující pravděpodobnost:
Tuto pravděpodobnost lze snadno vypočítat pomocí distribuční funkce :
Cvičení 3
Jaká je pravděpodobnost, že náhodná proměnná je menší než očekávaná hodnota, pokud má exponenciální rozdělení s parametrem ?
Očekávaná hodnota exponenciální náhodné proměnné s parametrem je Výše uvedenou pravděpodobnost lze vypočítat pomocí distribuční funkce :
Jak citovat
Citujte prosím jako: