College Algebra (Čeština)
Výsledky učení
- Určete vrchol, osu symetrie, průnik y a minimální nebo maximální hodnotu paraboly z je to graf.
- Určete kvadratickou funkci psanou v obecné a vrcholné podobě.
- Vzhledem k obecné kvadratické funkci najděte vrchol.
- Definujte doménu a rozsah kvadratické funkce určením vrcholu jako maxima nebo minima.
Grafem kvadratické funkce je křivka ve tvaru U, která se nazývá parabola. Jednou důležitou vlastností grafu je, že má extrémní bod, který se nazývá vrchol. Pokud se parabola otevře, vrchol představuje nejnižší bod v grafu nebo minimální hodnotu kvadratické funkce. Pokud se parabola otevře dolů, vrchol představuje nejvyšší bod v grafu nebo maximální hodnotu. V obou případech je vrchol bodem obratu v grafu. Graf je také symetrický se svislou čarou vedenou vrcholem, která se nazývá osa symetrie.
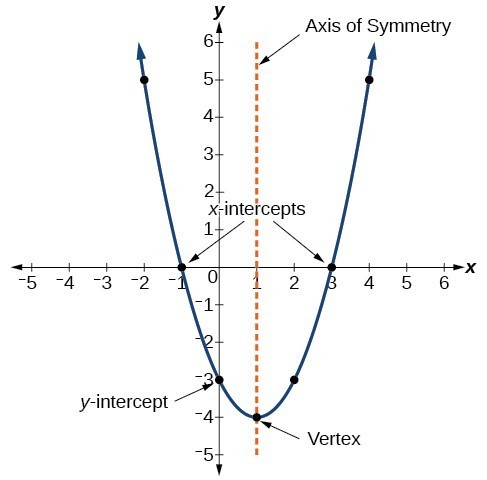
Rovnice kvadratických funkcí
Obecná forma kvadratické funkce představuje funkci ve tvaru
f \ left (x \ right) = a {x} ^ {2} + bx + c
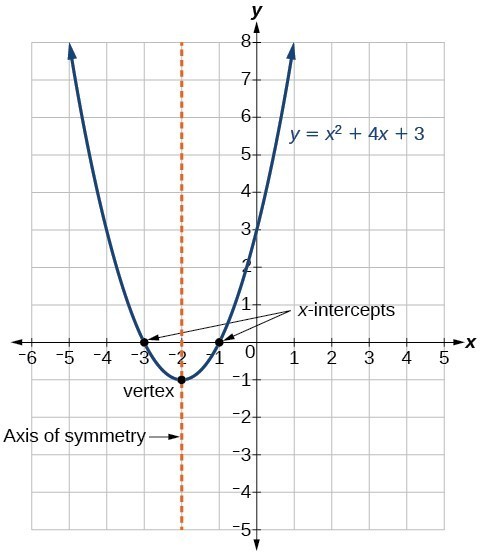
Standardní tvar kvadratické funkce představuje funkci ve tvaru
f \ left (x \ right) = a {\ left (xh \ right)} ^ {2} + k
Obecně kvadratická funkce najděte vrchol paraboly.
Jedním z důvodů, proč bychom chtěli identifikovat vrchol paraboly, je to, že tento bod nás bude informovat, kde se vyskytuje maximální nebo minimální hodnota výstupu, k a kde nastane, h. Pokud dostaneme obecnou formu kvadratické funkce:
f (x) = ax ^ 2 + bx + c
Můžeme definovat vrchol (h, k) provedením následujícího:
Vyhledání domény a rozsahu kvadratické funkce
Vstupní hodnotou kvadratické funkce může být jakékoli číslo. Doménou jakékoli kvadratické funkce jsou tedy všechna reálná čísla. Protože paraboly mají na vrcholu maximum nebo minimum, je rozsah omezen. Vzhledem k tomu, že vrchol paraboly bude buď maximální, nebo minimální, bude se rozsah skládat ze všech hodnot y větších nebo rovných souřadnicím y vrcholu nebo menších nebo rovných souřadnicím y v bodě obratu , podle toho, zda se parabola otevírá nahoru nebo dolů.
Přispějte!
Vylepšete tuto stránkuDalší informace