BFS vs DFS: Znát rozdíl

Co je BFS ?

BFS je algoritmus, který se používá ke grafování dat nebo prohledávání stromu nebo procházení struktur. Algoritmus efektivně navštíví a označí všechny klíčové uzly v grafu přesnou šířkou.

Tento algoritmus vybere v grafu jeden uzel (počáteční nebo zdrojový bod) a poté navštíví všechny uzly sousedící s vybraným uzlem. Jakmile algoritmus navštíví a označí počáteční uzel, posune se k nejbližším nenavštíveným uzlům a analyzuje je.

Po návštěvě jsou označeny všechny uzly. Tyto iterace pokračují, dokud nebudou úspěšně navštíveny a označeny všechny uzly grafu. Plnou formou BFS je vyhledávání na šířku.

V tomto BSF vs. Výukový program DFS Binární strom se naučíte:

• Co je BFS?
• Co je DFS?
• Příklad BFS
• Příklad DFS
• Rozdíl mezi BFS a binárním stromem DFS
• Aplikace BFS
• Aplikace DFS

Co je DFS?

DFS je algoritmus pro hledání nebo procházení grafů nebo stromů ve směru hloubky. Provedení algoritmu začíná v kořenovém uzlu a zkoumá každou větev před zpětným sledováním. Používá strukturu dat zásobníku, aby si pamatoval, získal následující vrchol a zahájil vyhledávání, kdykoli se v jakékoli iteraci objeví slepá ulička. Plnou formou DFS je vyhledávání do hloubky.

Příklad BFS

V následujícím příkladu DFS jsme použili graf se 6 vrcholy.

Příklad BFS

Krok 1)

Máte graf sedmi čísel od 0 do 6.

Krok 2)

0 nebo nula byla označena jako kořenový uzel.

Krok 3)

0 je navštíveno, označeno a vložen do datové struktury fronty.

Krok 4)

Zbývající 0 sousedních a nenavštívených uzly jsou navštíveny, označeny a vloženy do fronty.

Krok 5)

Traverské iterace se opakují, dokud všechny uzly jsou navštíveny.

Příklad DFS

V následujícím příkladu DFS jsme použili neorientovaný graf s 5 vrcholy.

Krok 1)

Začali jsme od vrcholu 0. Algoritmus začíná vložením do navštíveného seznamu a současným vložením všech jeho sousedních vrcholů do dat struktura zvaná zásobník.

Krok 2)

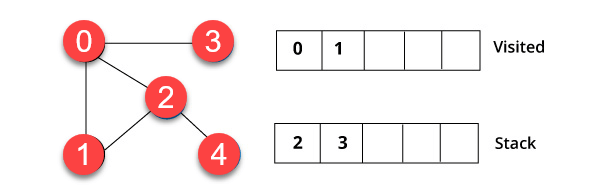
Navštívíte prvek , který je v horní části zásobníku, například 1, a přejděte do jeho sousedních uzlů. Je to proto, že 0 již byla navštívena. Proto navštěvujeme vrchol 2.

Krok 3)

Vertex 2 má nenavštívený blízký vrchol v 4. Proto přidáme, že v zásobníku a navštívit jej.

Krok 4)

Nakonec navštívíme poslední vrchol 3, nemá žádné nenavštívené sousední uzly. Prochod grafu jsme dokončili pomocí algoritmu DFS.

Rozdíl mezi BFS a DFS binárním stromem

BFS	DFS
BFS najde nejkratší cestu k cíli.	DFS přejde na konec podstromu a poté se vrátí zpět .
Plná forma BFS je Breadth-First Search.	Plná forma DFS je Depth First Search.
Používá frontu ke sledování dalšího místa k návštěvě.	Používá zásobník ke sledování dalšího místa k návštěvě.
BFS prochází podle úrovně stromu.	DFS prochází podle hloubky stromu.
Je implementován pomocí FI Seznam FO.	Implementuje se pomocí seznamu LIFO.
Ve srovnání s DFS vyžaduje více paměti.	Ve srovnání s BFS vyžaduje méně paměti.
Tento algoritmus poskytuje řešení pro mělkou cestu.	Tento algoritmus nezaručuje řešení nejmělčí cesty.
V BFS není třeba zpětné sledování.	Existuje potřeba zpětného sledování v DFS.
Nikdy nemůžete být uvězněni v konečných smyčkách.	Můžete být uvězněni v nekonečných smyčkách.
Pokud nenajdete žádný cíl, možná budete muset před nalezením řešení rozbalit mnoho uzlů.	Pokud nenajdete žádný cíl, může být zpětné sledování listového uzlu nastat.

Aplikace BFS

Zde jsou aplikace BFS:

Nevážené Grafy:

Algoritmus BFS může snadno vytvořit nejkratší cestu a minimální kostru, aby mohl s vysokou přesností navštívit všechny vrcholy grafu v co nejkratším čase.

Sítě P2P:

BFS lze implementovat k vyhledání všech nejbližších nebo sousedních uzlů v síti typu peer to peer. Tím vyhledáte požadovaná data rychleji.

Webové prohledávače:

Vyhledávací stroje nebo webové prohledávače mohou snadno vytvářet více úrovní indexů pomocí BFS. Implementace BFS začíná od zdroje, kterým je webová stránka, a poté navštíví všechny odkazy z tohoto zdroje.

Síťové vysílání:

Vysílaný paket je veden algoritmem BFS k nalezení a dosažení všech uzlů, pro které má adresu.

Aplikace DFS

Zde jsou důležité aplikace DFS:

Vážený graf:

Ve váženém grafu generuje traversal grafu DFS nejkratší strom cesty a minimální kostra.

Detekce cyklu v grafu:

Graf má cyklus, pokud jsme během DFS našli zadní hranu. Proto bychom měli pro graf spustit DFS a ověřit zadní hrany.

Hledání cesty:

Můžeme se specializovat na algoritmus DFS pro hledání cesty mezi dvěma vrcholy.

Topologické řazení:

Používá se primárně pro plánování úloh z daných závislostí mezi skupinou úloh. V počítačové vědě se používá při plánování instrukcí, serializaci dat, logické syntéze, určování pořadí úkolů kompilace.

Hledání silně propojených komponent grafu:

Používá se v grafu DFS, když existuje cesta z každého vrcholu v grafu k dalším zbývajícím vrcholům.

Řešení hádanek pouze s jedním řešením:

Algoritmus DFS lze snadno přizpůsobit prohledávání všech řešení bludiště zahrnutím uzlů na existující cestě v navštívené sadě.