College-Algebra (Deutsch)
Lernergebnisse
- Identifizieren Sie den Scheitelpunkt, die Symmetrieachse, den y-Achsenabschnitt und den minimalen oder maximalen Wert einer Parabel aus Es ist ein Diagramm.
- Identifizieren Sie eine quadratische Funktion, die in allgemeiner und Scheitelpunktform geschrieben ist.
- Suchen Sie bei gegebener quadratischer Funktion in allgemeiner Form den Scheitelpunkt.
- Definieren Sie die Domäne und Bereich einer quadratischen Funktion durch Identifizieren des Scheitelpunkts als Maximum oder Minimum.
Der Graph einer quadratischen Funktion ist eine U-förmige Kurve, die als Parabel bezeichnet wird. Ein wichtiges Merkmal des Diagramms ist, dass es einen Extrempunkt hat, der als Scheitelpunkt bezeichnet wird. Wenn sich die Parabel öffnet, repräsentiert der Scheitelpunkt den niedrigsten Punkt im Diagramm oder den Minimalwert der quadratischen Funktion. Wenn sich die Parabel öffnet, repräsentiert der Scheitelpunkt den höchsten Punkt im Diagramm oder den Maximalwert. In beiden Fällen ist der Scheitelpunkt ein Wendepunkt im Diagramm. Der Graph ist auch symmetrisch mit einer vertikalen Linie, die durch den Scheitelpunkt gezogen wird und als Symmetrieachse bezeichnet wird.
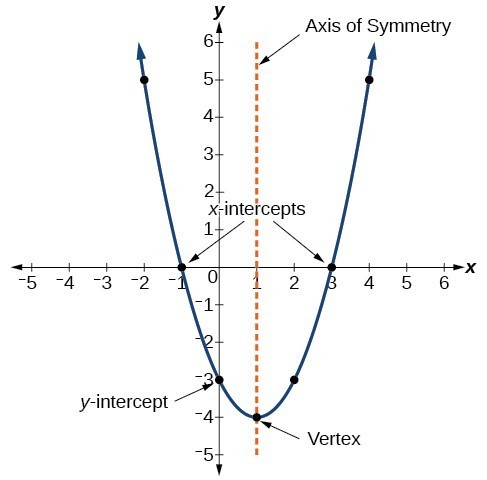
Gleichungen quadratischer Funktionen
Die allgemeine Form einer quadratischen Funktion präsentiert die Funktion in der Form
f \ left (x \ right) = a {x} ^ {2} + bx + c
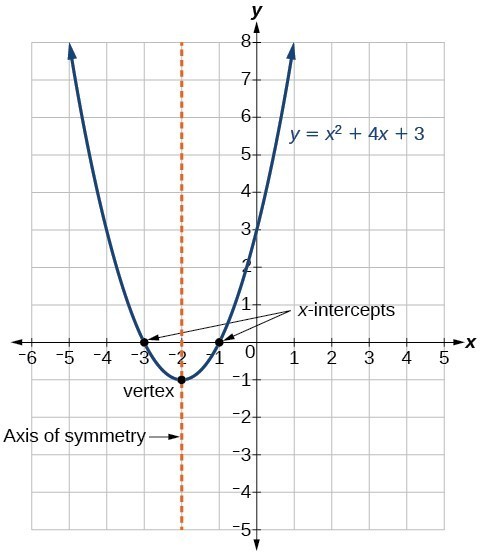
Die Standardform einer quadratischen Funktion präsentiert die Funktion in der Form
f \ left (x \ right) = a {\ left (xh \ right)} ^ {2} + k
Bei einer quadratischen Funktion im Allgemeinen Form, finden Sie den Scheitelpunkt der Parabel.
Ein Grund, warum wir den Scheitelpunkt der Parabel identifizieren möchten, ist, dass dieser Punkt uns informiert, wo der maximale oder minimale Wert der Ausgabe auftritt, k, und wo es tritt auf, h. Wenn wir die allgemeine Form einer quadratischen Funktion erhalten:
f (x) = ax ^ 2 + bx + c
Wir können definieren den Scheitelpunkt (h, k), indem Sie Folgendes tun:
Ermitteln der Domäne und des Bereichs einer quadratischen Funktion
Jede Zahl kann der Eingabewert einer quadratischen Funktion sein. Daher ist die Domäne jeder quadratischen Funktion alle reellen Zahlen. Da Parabeln am Scheitelpunkt ein Maximum oder ein Minimum haben, ist der Bereich eingeschränkt. Da der Scheitelpunkt einer Parabel entweder ein Maximum oder ein Minimum ist, besteht der Bereich aus allen y-Werten, die größer oder gleich der y-Koordinate des Scheitelpunkts oder kleiner oder gleich der y-Koordinate am Wendepunkt sind , je nachdem, ob sich die Parabel öffnet oder nicht.
Beitrag!
Verbessern Sie diese Seite. Erfahren Sie mehr