College-Algebra (Deutsch)
Wenn wir uns den Graphen einer rationalen Funktion ansehen, können wir ihr lokales Verhalten untersuchen und leicht erkennen, ob es Asymptoten gibt. Möglicherweise können wir sogar ihren Standort approximieren. Selbst ohne den Graphen können wir jedoch immer noch bestimmen, ob eine gegebene rationale Funktion Asymptoten aufweist, und ihre Position berechnen.
Vertikale Asymptoten
Die vertikalen Asymptoten einer rationalen Funktion können sein gefunden durch Untersuchen der Faktoren des Nenners, die den Faktoren im Zähler nicht gemeinsam sind. Vertikale Asymptoten treten an den Nullen solcher Faktoren auf.
Gewusst wie: Identifizieren Sie bei gegebener rationaler Funktion alle vertikalen Asymptoten ihres Graphen.
- Faktor Zähler und Nenner.
- Beachten Sie alle Einschränkungen im Bereich der Funktion.
- Reduzieren Sie den Ausdruck, indem Sie gemeinsame Faktoren im Zähler und im Nenner aufheben.
- Beachten Sie alle Werte Dies führt dazu, dass der Nenner in dieser vereinfachten Version Null ist. Hier treten die vertikalen Asymptoten auf.
- Beachten Sie alle Einschränkungen in der Domäne, in der keine Asymptoten auftreten. Dies sind entfernbare Diskontinuitäten.
Entfernbare Diskontinuitäten
Gelegentlich enthält ein Diagramm ein Loch: einen einzelnen Punkt, an dem das Diagramm nicht definiert ist, angezeigt durch ein offener Kreis. Wir nennen ein solches Loch eine entfernbare Diskontinuität.
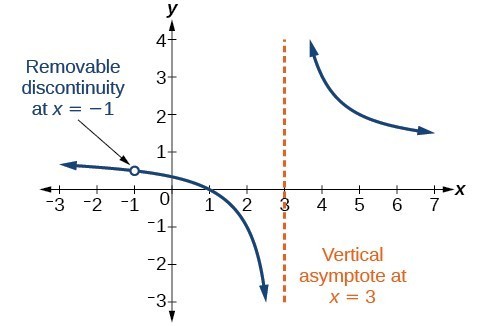
Abbildung 10
Allgemeiner Hinweis: Entfernbare Diskontinuitäten rationaler Funktionen
Eine entfernbare Diskontinuität tritt im Diagramm einer rationalen Funktion auf bei x = a, wenn a eine Null für einen Faktor im Nenner ist, der mit einem Faktor im Zähler gemeinsam ist. Wir faktorisieren Zähler und Nenner und prüfen auf gemeinsame Faktoren. Wenn wir einen finden, setzen wir den gemeinsamen Faktor auf 0 und lösen. Dies ist der Ort der entfernbaren Diskontinuität. Dies gilt, wenn die Multiplizität dieses Faktors größer oder gleich der im Nenner ist. Wenn die Multiplizität dieses Faktors im Nenner größer ist, gibt es bei diesem Wert immer noch eine Asymptote.
Horizontale Asymptoten
Während vertikale Asymptoten das Verhalten von a beschreiben Wenn die Ausgabe sehr groß oder sehr klein wird, beschreiben horizontale Asymptoten das Verhalten eines Diagramms, wenn die Eingabe sehr groß oder sehr klein wird. Denken Sie daran, dass das Endverhalten eines Polynoms das des Leitbegriffs widerspiegelt. Ebenso spiegelt das Endverhalten einer rationalen Funktion das Verhältnis der führenden Terme der Zähler- und Nennerfunktionen wider.
Bei der Überprüfung auf horizontale Asymptoten gibt es drei unterschiedliche Ergebnisse:
Fall 1: Wenn der Grad des Nenners > Grad des Zählers ist, gibt es eine horizontale Asymptote bei y = 0.

Fall 2: Wenn der Grad des Nenners < Grad des Zählers um eins ist, erhalten wir eine schräge Asymptote.

Beachten Sie, dass der Graph einer rationalen Funktion niemals eine vertikale Asymptote kreuzen wird, die Grafik kann eine horizontale oder nicht kreuzen schräge Asymptote. Auch wenn der Graph einer rationalen Funktion viele vertikale Asymptoten haben kann, hat der Graph höchstens eine horizontale (oder schräge) Asymptote.
Es sollte beachtet werden, dass, wenn der Grad des Zählers größer ist als der Grad des Nenners um mehr als eins ahmt das Endverhalten des Graphen das Verhalten des reduzierten Endverhaltensanteils nach. Wenn wir zum Beispiel die Funktion
mit Endverhalten
Das Endverhalten des Graphen würde dem eines geraden Polynoms mit einem positiven Leitkoeffizienten ähnlich sehen. P. >
Ein allgemeiner Hinweis: Horizontale Asymptoten von Rationale Funktionen
Die horizontale Asymptote einer rationalen Funktion kann durch Betrachten der Grade von Zähler und Nenner bestimmt werden.
- Der Grad des Zählers ist kleiner als der Grad des Nenners: horizontale Asymptote bei y = 0.
- Der Grad des Zählers ist um eins größer als der Grad des Nenners: keine horizontale Asymptote; schräge Asymptote.
- Der Grad des Zählers entspricht dem Grad des Nenners: horizontale Asymptote im Verhältnis der führenden Koeffizienten.
Ein allgemeiner Hinweis: Abschnitte rationaler Funktionen
Eine rationale Funktion hat einen y-Abschnitt, wenn die Eingabe Null ist, wenn die Funktion ist bei Null definiert. Eine rationale Funktion hat keinen y-Achsenabschnitt, wenn die Funktion nicht bei Null definiert ist.
Ebenso hat eine rationale Funktion x-Achsenabschnitte an den Eingängen, die bewirken, dass der Ausgang Null ist. Da ein Bruch nur dann gleich Null ist, wenn der Zähler Null ist, können x-Abschnitte nur auftreten, wenn der Zähler der rationalen Funktion gleich Null ist.
Try It 7
Wenn die reziproke Quadratfunktion um 3 Einheiten nach rechts und um 4 Einheiten nach unten verschoben ist, schreiben Sie dies als rationale Funktion. Suchen Sie dann die x- und y-Abschnitte sowie die horizontalen und vertikalen Asymptoten.
Lösung