BFS vs DFS: Kennen Sie den Unterschied

Was ist BFS? ?

BFS ist ein Algorithmus, der zum Zeichnen von Daten oder zum Suchen von Bäumen oder zum Durchlaufen von Strukturen verwendet wird. Der Algorithmus besucht und markiert effizient alle Schlüsselknoten in einem Diagramm in einer genauen Breite.

Dieser Algorithmus wählt einen einzelnen Knoten (Anfangs- oder Quellpunkt) in einem Diagramm aus und besucht dann alle Knoten neben dem ausgewählten Knoten. Sobald der Algorithmus den Startknoten besucht und markiert, bewegt er sich zu den nächsten nicht besuchten Knoten und analysiert diese.

Nach dem Besuch werden alle Knoten markiert. Diese Iterationen werden fortgesetzt, bis alle Knoten des Diagramms erfolgreich besucht und markiert wurden. Die vollständige Form von BFS ist die Breitensuche.

In diesem BSF Vs. Im DFS-Tutorial zum Binärbaum lernen Sie:

• Was ist BFS?
• Was ist DFS?
• Beispiel für BFS
• Beispiel für DFS
• Unterschied zwischen BFS und DFS-Binärbaum
• Anwendungen von BFS
• Anwendungen von DFS

Was ist DFS?

DFS ist ein Algorithmus zum Suchen oder Durchlaufen von Graphen oder Bäumen in Tiefenrichtung. Die Ausführung des Algorithmus beginnt am Wurzelknoten und untersucht jeden Zweig vor dem Zurückverfolgen. Es verwendet eine Stapeldatenstruktur, um sich zu merken, den nachfolgenden Scheitelpunkt abzurufen und eine Suche zu starten, wenn in einer Iteration eine Sackgasse auftritt. Die vollständige Form von DFS ist die Tiefensuche.

Beispiel für BFS

Im folgenden Beispiel für DFS werden wir habe einen Graphen mit 6 Eckpunkten verwendet.

Beispiel für BFS

Schritt 1)

Sie haben ein Diagramm mit sieben Zahlen im Bereich von 0 bis 6.

Schritt 2)

0 oder Null wurde als Wurzelknoten markiert.

Schritt 3)

0 wird besucht und markiert und in die Warteschlangendatenstruktur eingefügt.

Schritt 4)

Verbleibende 0 nebeneinander und nicht besucht Knoten werden besucht, markiert und in die Warteschlange eingefügt.

Schritt 5)

Durchlaufende Iterationen werden bis wiederholt Alle Knoten werden besucht.

Beispiel für DFS

Im folgenden Beispiel für DFS haben wir einen ungerichteten Graphen mit 5 Eckpunkten verwendet.

Schritt 1)

Wir haben mit Scheitelpunkt 0 begonnen. Der Algorithmus beginnt damit, ihn in die besuchte Liste aufzunehmen und gleichzeitig alle benachbarten Scheitelpunkte in die Daten aufzunehmen Struktur namens Stapel.

Schritt 2)

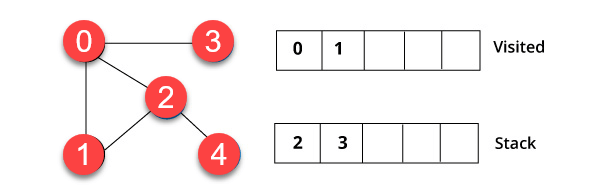
Sie besuchen das Element , die sich am oberen Rand des Stapels befindet, z. B. 1, und zu den benachbarten Knoten gehen. Dies liegt daran, dass 0 bereits besucht wurde. Daher besuchen wir Scheitelpunkt 2.

Schritt 3)

Vertex 2 hat in 4 einen nicht besuchten nahe gelegenen Vertex. Daher fügen wir diesen in den Stapel ein und besuchen ihn.

Schritt 4)

Schließlich werden wir besuchen Der letzte Scheitelpunkt 3 hat keine nicht besuchten benachbarten Knoten. Wir haben die Durchquerung des Graphen mit dem DFS-Algorithmus abgeschlossen.

Unterschied zwischen BFS- und DFS-Binärbaum

BFS	DFS
BFS findet den kürzesten Pfad zum Ziel.	DFS wird am Ende eines Teilbaums angezeigt und anschließend zurückverfolgt
Die vollständige Form von BFS ist die Breitensuche.	Die vollständige Form der DFS ist die Tiefensuche.
Es verwendet eine Warteschlange, um den nächsten zu besuchenden Ort zu verfolgen.	Es verwendet einen Stapel, um den nächsten zu besuchenden Ort zu verfolgen.
BFS wird gemäß der Baumebene durchlaufen.	DFS wird gemäß der Baumtiefe durchlaufen.
Es wird mithilfe von FI implementiert FO-Liste.	Es wird mithilfe der LIFO-Liste implementiert.
Im Vergleich zu DFS ist mehr Speicher erforderlich.	Im Vergleich zu BFS wird weniger Speicher benötigt.
Dieser Algorithmus bietet die flachste Pfadlösung.	Dieser Algorithmus garantiert nicht die Lösung mit dem flachsten Pfad.
In BFS ist kein Backtracking erforderlich.	Es gibt Backtracking in DFS erforderlich.
Sie können niemals in endlichen Schleifen gefangen werden.	Sie können in Endlosschleifen gefangen sein.
Wenn Sie kein Ziel finden, müssen Sie möglicherweise viele Knoten erweitern, bevor die Lösung gefunden wird.	Wenn Sie kein Ziel finden, kann das Zurückverfolgen von Blattknoten erfolgen auftreten.

Anwendungen von BFS

Hier sind Anwendungen von BFS:

Ungewichtet Diagramme:

Der BFS-Algorithmus kann auf einfache Weise den kürzesten Pfad und einen minimalen Spannbaum erstellen, um alle Scheitelpunkte des Diagramms in kürzester Zeit mit hoher Genauigkeit zu besuchen.

P2P-Netzwerke:

BFS kann implementiert werden, um alle nächsten oder benachbarten Knoten in einem Peer-to-Peer-Netzwerk zu lokalisieren. Dadurch werden die erforderlichen Daten schneller gefunden.

Webcrawler:

Suchmaschinen oder Webcrawler können mithilfe von BFS problemlos mehrere Indexebenen erstellen. Die BFS-Implementierung beginnt bei der Quelle, der Webseite, und besucht dann alle Links von dieser Quelle.

Netzwerk-Broadcasting:

Ein gesendetes Paket wird vom BFS-Algorithmus geleitet, um alle Knoten zu finden und zu erreichen, für die es die Adresse hat.

Anwendungen von DFS

Hier sind wichtige Anwendungen von DFS:

Gewichteter Graph:

In einem gewichteten Graph wird die DFS-Graph-Durchquerung generiert der kürzeste Pfadbaum und der minimale Spannbaum.

Erkennen eines Zyklus in einem Diagramm:

Ein Diagramm hat einen Zyklus, wenn während der DFS eine Hinterkante gefunden wurde. Daher sollten wir DFS für das Diagramm ausführen und die Hinterkanten überprüfen.

Pfadfindung:

Wir können uns auf den DFS-Algorithmus spezialisieren, um einen Pfad zwischen zwei Scheitelpunkten zu suchen.

Topologische Sortierung:

Sie wird hauptsächlich zum Planen von Jobs aus den angegebenen Abhängigkeiten innerhalb der Jobgruppe verwendet. In der Informatik wird es bei der Befehlsplanung, Datenserialisierung, Logiksynthese und Bestimmung der Reihenfolge von Kompilierungsaufgaben verwendet.

Durchsuchen stark verbundener Komponenten eines Diagramms:

Wird im DFS-Diagramm verwendet, wenn ein Pfad von jedem Scheitelpunkt im Diagramm zu anderen verbleibenden Scheitelpunkten vorhanden ist.

Lösen von Rätseln mit nur einer Lösung:

Der DFS-Algorithmus kann einfach angepasst werden, um alle Lösungen für ein Labyrinth zu suchen, indem Knoten auf dem vorhandenen Pfad in die besuchte Gruppe aufgenommen werden.