Berechnen des Volumens
Berechnen des Volumens
Das Volumen wird in Würfeln (oder Kubikeinheiten) gemessen.

Wie viele Würfel enthält dieses rechteckige Prisma (Quader)?
Wir können zählen die Würfel, obwohl es schneller ist, die Länge, Breite und Höhe zu nehmen und Multiplikation zu verwenden. Das obige rechteckige Prisma hat ein Volumen von 48 Kubikeinheiten.
Das Volumen eines rechteckigen Prismas beträgt = Länge x Breite x Höhe
Beispiele für die Berechnung der Fläche eines Rechtecks
Wir müssen zwei Multiplikationen durchführen, um die Lautstärke zu berechnen. Wir berechnen die Fläche einer Fläche (oder Seite) und multiplizieren diese mit ihrer Höhe. Die folgenden Beispiele zeigen, wie es drei Möglichkeiten gibt.
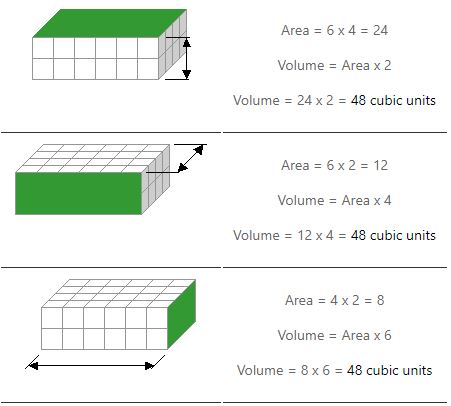
Beachten Sie, wie wir die gleiche Antwort erhalten, egal auf welcher Seite wir einen Bereich finden.
Wenn Ihr Kind anfängt, mit Bereich und Umfang zu arbeiten, arbeitet es normalerweise mit zwei Dimensionen – Quadrate, Rechtecke, Dreiecke usw., die auf Papier als flach angezeigt werden – es gibt keine Tiefe oder 3. Dimension. Das Arbeiten mit Volumen umfasst drei Dimensionen. Stellen Sie sicher, dass Ihr Kind sich dessen bewusst ist und die Würfel und andere auf Papier gezeigte 3D-Formen nicht als eine weitere „Form auf der Seite“ betrachtet. Zeigen Sie ihnen echte Kästchen und zeigen Sie, wie diese auf einem zweidimensionalen Blatt Papier gezeichnet (oder dargestellt) werden können. Mit anderen Worten, stellen Sie sicher, dass die Verbindung zwischen dem, was auf dem Papier steht, und dem, was es in der realen Welt darstellt, hergestellt wird.
Stellen Sie sicher, dass Ihr Kind nicht durch die Verwendung der Lautstärke verwirrt wird, wenn Sie über Lautstärke sprechen
Einheiten zur Volumenmessung
Es gibt sehr große Unterschiede zwischen Maßeinheiten für das Volumen. Beispielsweise gibt es 100 Zentimeter in 1 Meter, aber 1.000.000 (ja, 1 Million) ) Kubikzentimeter in Kubikmetern.
Warum der große Unterschied? Weil wir nicht nur Länge, sondern auch Länge, Breite und Höhe haben. Das folgende Beispiel für Zuckerwürfel zeigt dies.
Wie viel Zucker? 1 m3 oder 1.000.000 cm3
Stellen Sie sich vor, Sie füllen eine sehr große Kiste (1 Meter breit, 1 Meter lang und 1 Meter hoch) mit Zuckerwürfeln (jeweils) Seite 1 Zentimeter).
 |
Schritt 1: Eine Zeile am unteren Rand des Felds – das wären 100 Zuckerwürfel |
| Schritt 2: Decken Sie den Rest des Bodens der Schachtel ab – das würde insgesamt 100 Zeilen mit jeweils |
|
| Schritt 3: Wiederholen Sie diesen Vorgang 99 Mal, bis Schichten von 10.000 Würfeln, die 100 tief gestapelt sind. 10.000 x 100 = 1.000.000 Zuckerwürfel |
1 m3 enthält 1.000.000 cm3 – achten Sie darauf, nicht zu viel Zucker zu haben!
Es gibt andere Einheiten zur Volumenmessung. Kubikzoll, Kubikfuß, Kubikmeter sind alle Einheiten, die zur Volumenmessung verwendet werden. Milliliter, Liter, Gallonen werden auch besonders beim Messen von Flüssigkeiten verwendet.
Vergessen Sie nicht die kleinen 3
Wir schreiben kubische Größen mit einer kleinen 3 neben der Einheit.
Wir schreiben mm3, cm3, m3, km3, cm3
Wir können sagen „85 Zentimeter gewürfelt“ oder „85 Kubikzentimeter“
Beispiele für die Berechnung des Volumens rechteckiger Prismen
 |
Volumen = Länge x Breite x Höhe Volumen = 12 cm x 8 cm x 6 cm = 576 cm3 |
| Volumen = Länge x Breite x Höhe Volumen = 20 mx 2 mx 2 m = 80 m3 |
|
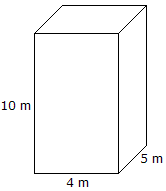 |
Volumen = Länge x Breite x Höhe Volumen = 10 mx 4 mx 5 m = 200 m3 |
Volumen eines Zylinders
Berechnung des Volumens eines Zylins Bei der Multiplikation wird die Fläche der Basis mit der Höhe des Zylinders multipliziert. Die Basis eines Zylinders ist kreisförmig und die Formel für die Fläche eines Kreises lautet: Fläche eines Kreises = πr2. Es gibt hier mehr auf der Fläche eines Kreises.
 |
Volumen = Grundfläche x Höhe Volumen = πr2 xh Volumen = πr2 h |
Hinweis: In den folgenden Beispielen Wir werden 3.14 als ungefähren Wert für π (Pi) verwenden.
Beispiel für die Berechnung des Volumens eines Zylinders
 Die Abmessungen sind in cm angegeben. |
Volumen = πr2 h Volumen = 3.14 x 3 x 3 x 8 Volumen = 226,08 cm3 |
Volumen eines Kegels
Das Volumen eines Kegels entspricht einem Drittel des Volumens eines Zylinders bei entsprechender Höhe und Fläche der Basis. Dies gibt die Formel für das Volumen eines Kegels wie unten gezeigt an.
 |
Volume = 1/3 πr2h |
Beispiel für die Berechnung des Volumens eines Kegels
 Die Abmessungen sind in cm angegeben. |
Volumen = 1/3 πr2 h Volumen = 1/3 x 3,14 x 2 x 2 x 7 Volumen = 29,31 cm3 |
Volumen einer Kugel
Die Formel für das Volumen einer Kugel ist unten dargestellt.
 |
Volume = 4/3 πr3 |
Beispiel für die Berechnung des Volumens einer Kugel
 Die Abmessungen sind in cm angegeben. |
Volumen = 4/3 πr3 Volumen = 4/3 x 3,14 x 4 x 4 x 4 Volumen = 267,95 cm3 |
Arbeitsblätter für druckbare Volumes
Verwenden Sie das folgende Arbeitsblatt, um die Berechnung von Volumina zu üben.
- Ermitteln des Volumens in kubischen Einheiten – rechteckige Prismen und Verbundwerkstoffe
- Volumen von rechteckigen Prismen
- Volumen von rechteckigen Prismen
- Volumen von „realen“ Objekten, z von Müslischachteln
- Berechnen von Volumina, z. von dreieckigen Prismen und Zylindern
Hier erhalten Sie andere Geometrie-Arbeitsblätter zu Umfang, Fläche und mehr.