Berechnen der Fläche
Berechnen der Fläche
Die Fläche wird in Quadraten (oder quadratischen Einheiten) gemessen.
Wie viele Quadrate befinden sich in diesem Rechteck?

Wir können die Quadrate zählen oder wir können Nehmen Sie die Länge und Breite und verwenden Sie die Multiplikation. Das obige Rechteck hat eine Fläche von 15 quadratischen Einheiten.
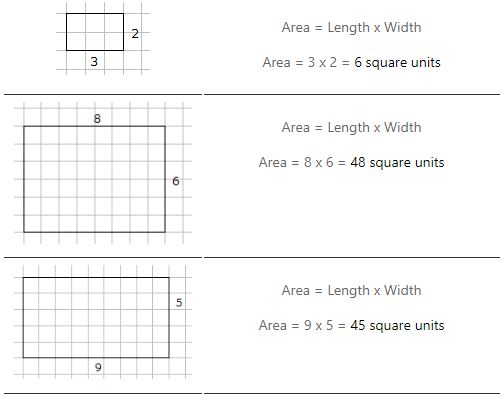
Die Fläche eines Rechtecks ist = Länge x Breite
Beispiele für die Berechnung der Fläche eines Rechtecks
Einheiten zum Messen der Fläche
Wir messen die Fläche mit Quadraten. Wir verwenden unterschiedliche Größen von Quadraten, je nachdem, wie groß oder klein eine Fläche ist.
| Beispiel | Seitenlänge auf Quadraten | Einheit |
| Größe der Nagel auf den Daumen | Millimeter | mm2 |
| Papiergröße | Zentimeter | cm2 |
| Größe eines Raums | Meter | m2 |
| Größe einer Stadt | Kilometer | km2 |
Vergessen Sie nicht die kleinen 2
Wir schreiben Quadratgrößen mit einer kleinen 2 neben der Einheit.
Wir schreiben mm2, cm2, m2, km2, cm2
Wir können „63 Millimeter im Quadrat“ oder „63 Quadratmillimeter“
sagen
Wir könnten kleine Quadrate verwenden, um große Flächen zu messen. Das einzige Problem dabei ist, dass wir am Ende sehr große verwenden müssten Zahlen. Beispielsweise könnte ein Feld mit 5.000.000.000 Quadratmillimetern gemessen werden, wenn 5.000 Quadratmeter viel einfacher zu sagen, zu schreiben und zu visualisieren wären.
Sie werden wahrscheinlich mehr Einheiten für die Messfläche hören. Quadratzoll, Quadratfuß, Quadratmeter, Quadratmeilen, Morgen, Hektar sind alle Einheiten, die zur Messung der Fläche verwendet werden.
Weitere Beispiele für die Berechnung der Fläche
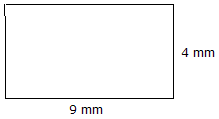 |
Fläche = Länge x Breite Fläche = 9 mm x 4 mm = 36 mm2 |
 |
Fläche = Länge x Breite Fläche = 7 cm x 6 cm = 42 cm2 |
 |
Fläche = Länge x Breite Fläche = 8 mx 2 m = 16 m2 |
 |
Fläche = Länge x Breite Fläche = 7 km x 5 km = 35 km2 |
Fläche eines Quadrats
Die Länge und Breite eines Quadrats sind gleich, daher müssen wir nur die Länge mit der Länge multiplizieren.
| Fläche = Länge x Länge Fläche = 6 cm x 6 cm = 36 cm2 |
Fläche eines Kreises
Die Fläche eines Kreises = πr2
Dabei ist r der Radius des Kreises und π das Verhältnis des Umfangs eines Kreises zu seinem Durchmesser.
π (ausgesprochen „pie“ und oft geschrieben „Pi“) ist eine unendliche Dezimalstelle mit einer gemeinsamen Annäherung von 3.14159. Mehr über Pi erfahren Sie hier
Beispiel für die Berechnung der Fläche eines Kreises
 |
Area = πr2 Area = 3.14159 x (4 cm) 2 Fläche = 3,14159 x 16 cm2 Fläche = 50,27 cm2 Antwort auf 2 Dezimalstellen gerundet |
Erläuterung der Fläche einer Kreisformel
Nehmen Sie einen Kreis und teilen Sie ihn in gleich große Sektoren und ordnen Sie diese wie unten gezeigt neu an. Beachten Sie, dass die Form mit zunehmender Verkleinerung der Sektoren eher einem Rechteck ähnelt. Hinweis: Es gibt keine Begrenzung dafür, wie klein diese Sektoren sein können und wie stark sie einem Rechteck ähneln können, wenn sie angeordnet sind.
Angenommen, wir wissen, dass der Umfang eines Kreises gleich 2πr ist, können wir Dimensionen hinzufügen das „Rechteck“ wie unten gezeigt. Anhand der Fläche einer Rechteckflächenformel, Fläche = Breite x Höhe, können wir sehen, wie unser Kreis, der als Rechteck neu konfiguriert wurde, eine Fläche aufweist, die ungefähr πr xr oder πr2
Kreis entspricht Sektoren neu angeordnet

Kreissektoren neu angeordnet – Starten wie ein Rechteck aussehen

Bereich von Zusammengesetzte Formen
Es gibt viele Fälle, in denen für die Berechnung einer Gesamtfläche mehr als eine Fläche berechnet werden muss, gefolgt von einer Addition, Subtraktion oder einer anderen Kombination von Operationen, um die erforderliche Fläche zu finden.
Hinweis: In den folgenden Beispielen werden die Maßeinheiten nicht angezeigt und die Antworten und der Wert von π (Pi) wurden auf das nächste Hundertstel gerundet.
Beispiel: Einfache zusammengesetzte Formen
Das folgende Beispiel für die Flächenberechnung ist relativ einfach. Die Form kann als Dreieck in Kombination mit einem Rechteck betrachtet werden.
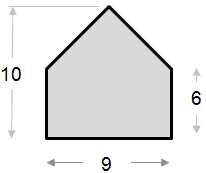 |
Fläche des Dreiecksteils: ½ x Basis x Höhe ½ x 9 x 4 = 18 Fläche des Rechteckteils: Gesamtfläche = 18 + 54 = 72 |
Das obige Beispiel zeigt eine allgemeine Anforderung beim Arbeiten mit Compound Formen – Abmessungen finden, die nicht angezeigt werden. Geben Sie bei der Nachhilfe Ihrer Kinder bei Bedarf Hilfe, um diese „fehlenden“ Dimensionen zu finden. Im Folgenden finden Sie ein weiteres Beispiel.
Ermitteln der Abmessungen
 |
Wie groß ist das kleine rechteckige Teil? Breite? 12 – 7 – 2 = 3 Höhe? 8 – 6 = 2 |
Beispiel: Subtrahieren eines Bereichs von einem anderen
Im folgenden Beispiel kann die Form als Rechteck mit einem ausgeschnittenen Dreieck betrachtet werden.
 |
Fläche des Rechteckteils: Breite x Höhe 5 x 6 = 30 Fläche des Dreiecksteils: Gesamtfläche = 30 – 4,50 = 25,50 |
Beispiel: Teilflächen
Das folgende Beispiel ähnelt dem obigen, obwohl wir, da wir einen Halbkreis haben, einen Bruch (eine Hälfte) berechnen müssen. Beachten Sie in diesem Beispiel den Durchmesser und nicht den Radius.
 |
Fläche des Dreiecksteils: ½ x Basis x Höhe ½ x 6 x 6 = 18 Fläche des Halbkreisteils: Gesamtfläche = 18 – 3,53 = 14,47 |
Beispiel: Entscheidungen! Kombinieren? Subtrahieren
Es ist üblich, mehr als eine Möglichkeit zur Berechnung der endgültigen Fläche zu haben. In den folgenden Beispielen kann die Form als zwei kombinierte Rechtecke oder als ein großes Rechteck mit einem kleineren Rechteck gesehen werden, das aus der oberen rechten Ecke „ausgeschnitten“ wird.
Berechnen von Arbeitsblättern
Drucken Lesen Sie die unten aufgeführten Arbeitsblätter aus und verwenden Sie sie zum Üben, wenn Sie Ihre Kinder unterrichten.
- Berechnen von Bereichen – Rechtecke und Quadrate
- Berechnen von Bereichen – Rechtecken
- Berechnen Bereiche – Rechtecke
- Berechnen von zusammengesetzten Bereichen, z mit rechteckigen Formen
- Berechnen von zusammengesetzten Bereichen, z. mit Rechtecken, Dreiecken und Kreisen
- Berechnen von Bereichen, z. von Dreiecken
- Fläche eines Kreises
- Berechnen von Oberflächenbereichen, z. von rechteckigen Prismen
Weitere druckbare Geometrie-Arbeitsblätter finden Sie hier.